Funciones lineales.

Definición de función lineal.

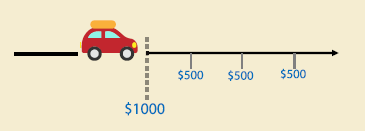
Viajando por Cancún, unos amigos decidieron rentar un carro para conocer la mejor ciudad. La renta del carro les costó $1,000, pero por cada 100km recorridos se les cobrará $500 adicionales.

 

Seguramente, notaste de que este caso se refiere a una relación que además es una función.

Esta función puede ser representada como:

·         1,000 es el importe inicial que pagaron por la renta.

·         X representa la cantidad de veces que recorren 100km, por lo tanto 500 representa la multiplicación del costo de 500 pesos por cada 100km recorridos.

La función lineal representa la relación de la situación planteada como se conoce como función lineal.

Una función lineal es una función de primer grado; es decir, el exponente de la literal es 1 y para graficarla se representa como una línea recta.

Las funciones lineales tienen la forma:

Donde m y b son constantes reales y x es la variable independiente y se conoce como factor de desplazamiento.

La constante representa a la pendiente de la recta, es decir, la inclinación. Observa en las siguientes gráficas de funciones como la inclinación de la recta aumenta cuando se eleva el valor de m de 0.5 a 1.5.

La constante b es el punto de corte de la recta con el eje y.

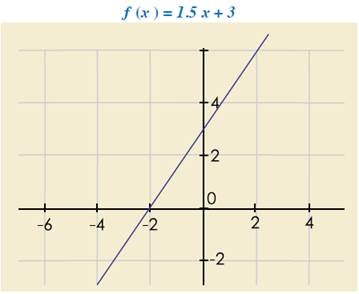
Observa las gráficas de las siguientes funciones. En la primera, la recta corta el eje y en 2; en la segunda, la corta en 4.

Ejemplos de funciones lineales.

Gráfica de una función lineal.

Una característica de la función lineal es que al graficarla se produce una línea recta.

Se graficará la función lineal:

Para graficar funciones lineales se utilizará el software de la pagina www.fooplot.com

1.       Ingresa a la página

2.       Identifica el siguiente recuadro.

3.       Escribe la ecuación 5x+10

4.       Presione la tecla <Enter> o <Intro> en el teclado de tu computadora.

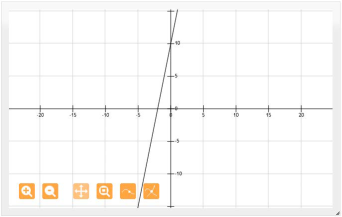
5.       Observa la gráfica.

6.       Puedes exportar la imagen de la gráfica en la siguiente sección del sitio.

Ejemplo.

¿La función f(x)=x²+3, es lineal?

La función no es lineal porque:

·         No tiene la forma y=mx+b

·         No es de primer grado

·         Al graficarla no se produce una línea recta.

Funciones Lineales

Velocidad de un automóvil

Son muchas las definiciones que se pueden dar para aclarar el concepto de velocidad. Posiblemente, lo primero que se piensa para explicar qué es la velocidad es “cubrir una distancia en el menor tiempo posible”. Esta definición ofrece una idea general de dicho concepto. Ahora bien, a lo largo de este apartado podrás ver que la velocidad es una cantidad física.

Cuando alguien viaja en automóvil se pregunta cuánto tardó, por ejemplo, una hora, en recorrer una distancia, 100 km. Se suele decir que se viajó, si es el caso, a 120 km/h. Sin embargo, el velocímetro no permaneció fijo indicando 120 km/h durante todo el viaje: el automóvil arrancó, frenó y aceleró para pasar a otro lugar. Al hacer una estimación de este tipo, se suele calcular la velocidad promedio del coche, pero no se considera la velocidad en cada instante del viaje, a la cual se puede llamar velocidad instantánea o, simplemente, velocidad.

La velocidad promedio o media se suele calcular como: Por ejemplo, si se mantiene una velocidad constante de 120 km/h todo el tiempo se sabe que el recorrido será de 120 km en una hora, 60 km en 30 minutos, 20 km en 15 minutos, 240 km en 120 minutos, así sucesivamente.

En la siguiente imagen (gráfica) se muestran algunos de los puntos:

La variable independiente, o sea el dominio de la función, es la t que se encuentra en el eje x y la variable dependiente es y, la cual representa la distancia o el espacio recorrido.

La ecuación que describe este fenómeno se representa como una línea recta. Por su parte, la forma general de la función es la siguiente:

ax + by = c

Otra forma en que se puede representar esta función es con la ordenada al origen, dada por:

y = mx + b

Donde el término independiente b se llama ordenada al origen y t es la pendiente de la recta. Ahora bien, la que describen los puntos de la gráfica mostrada anteriormente está dada por:

y = m · t

Ahora la ecuación y = m · t tiene la forma de la ecuación y = mx + b, la cual tiene pendiente y ordenada al origen. Es decir, si la velocidad es cero y también t = 0, se obtiene y = b, esto significa que si se conoce la posición inicial (b), que llamamos b o y la velocidad (v) del automóvil, la ecuación de la recta queda definida por:

y = v · t + b₀

Si observas con atención identificarás que se trata de una ecuación lineal, ya que la variable y solo depende del tiempo (t) si la velocidad es constante o se calcule una velocidad media. El término b₀, por lo tanto, representa la posición inicial del automóvil. Dicho de manera coloquial, para lograr una velocidad constante de 120 km/h el punto de partida del conteo debe ser cuando el automóvil alcance esa velocidad

El automóvil se encuentra en una posición inicial para comenzar su movimiento en forma recta.

Un movimiento en este caso va a depender de las constantes: posición y velocidad, donde el comportamiento de éstas determina el de las demás.

Función lineal. Es una función polinómica de primer grado que se representa en una gráfica como una línea recta y se escribe como:

ƒ (x) = m · x + b₀ y = m · x + b

Recuerda, los polinomios de primer grado tienen la variable elevada a la primera potencia; y cuando la potencia es uno no se escribe:

ƒ (x) = m · x1 + b

Donde m es la pendiente de la recta, la constante b es el punto de cruce de la recta con el eje Y y la variable es x. Ejemplos:

Funciones lineales

Las funciones lineales tiene como expresión analítica una ecuación de primer grado, en las siguientes pueden ponerse F (X) o (y).

                                                          

Graficamos la función a) tabulando: le podremos dar valores a X, se hacen la operación indicada para obtener el correspondiente valor de Y. Los valores (X, Y) son entonces puntos coordenados que se localizaban en el plano.

Localizando los puntos (X, Y) en el plano y uniendolos se obtiene en la siguiente gráfica.

Ejemplos:

Tiempo (X)	$ (Y)
0	0
1	5
2	10
3	15
4	20

                                                                                        

Si (X) representan los minutos por llamadas y (Y) el costo de la renta del celular podemos establecer que para y=5x, por cada minuto pagarás $5.00

Tiempo (X)	$(y)
0	10
1	12
2	14
3	16
4	18

La razón del cambio es 2 (por cada minuto, el costo aumenta dos), pero a partir de un costo inicial de $10.00. Ese costo inicial se verá en la gráfica como la intersección con el eje y porque cuando  x=0, y=10

                                                                                                   

Analizando las tablas y la práctica se puede concluir que … Aun cuando la primera función el costo por llamada es más alto ($5) en los primeros 5 minutos del primer plan sale más barato. Pero llega un momento en que el segundo plan de la segunda función no se cobra un costo inicial de $10, después del tercer minuto ya nos conviene más.

También podríamos preguntarnos cuál sería el costo en fracciones de minutos. Por ejemplo, el minuto 1.5, el primer plan de la primera función nos costaría y=5(1.5)=7.5.

Y en el segundo plan de la segunda función nos costará y=2(1.5)+10=13

Características de la función lineal

una función lineal, cuya gráfica es una recta, la razón de cambio (cambio en Y entre cambio en X) es constante. Su valor numérico, se le llama la pendiente de la recta. Esa relación de cambio es válida para todas las rectas y entre cualquier par de puntos. para ejemplificar retomemos los valores anteriores a la cual le agregamos dos columnas:

1.       ¿cuándo cambiaría X?

2.       ¿Y cuánto cambiaría Y?

en la primera y cuarta columna de la tabla:

X cambio de 1 (de -4 a -3)

Y cambio de 5 (de -18 a -13)

Cambio en X	X	Y	Cambio de Y
	-4	-18	5
1	-3	-13	5
1	-2	-8	5
1	-1	-3	5
1	0	2	5
1	1	7	5
1	2	12	5

La relación de cambio de Y con respecto a X es 5

                                                                             

Y esa cantidad (cinco) está indicada en la función f(x)=5x+2

La razón de cambio en la gráfica tomando los valores (0,2) y (2,12), se visualiza en la siguiente forma.

Algunos ejemplos donde la relación entre las variables trece o de trece siempre con la misma razón de cambio y que son modelados son: medición del tiempo y tablas de precios.