Concepto de potencia.
De la potencia aún no hay cosas que se deben de
conocer. Algunos usos cotidianos de este concepto Puedes encontrarlo en la
noticias del día. un ejemplo son los carros: ¿Cuál es el carro más potente y
cuál es el menos potente del mundo?
![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg5OvXtxRYoJ59ROLE_hIn4oeyMnrupCRD14r-p-lWiwEmM4ETKQ0OL5m04hiSWbrVWDKFX6ZBg0lMdDX0_ACTcJFNXBftJWnv9tfNeBC9JGu4DVW_DyE-HQgdNOwk7WohXcl3Sivjf70PE/?imgmax=800) El
Seat Mii es el coche más pequeño de la gama Seat y un hermano clónico de
Volkswagen Up! y el Škoda CitiGo. Es un producto urbano con una longitud de 3.
56 m Y usa un motor cilíndrico de gasolina De 60 CV asociado a una caja de
cambios de cinco velocidades.
El
Seat Mii es el coche más pequeño de la gama Seat y un hermano clónico de
Volkswagen Up! y el Škoda CitiGo. Es un producto urbano con una longitud de 3.
56 m Y usa un motor cilíndrico de gasolina De 60 CV asociado a una caja de
cambios de cinco velocidades.
Koenigsegg One:1, Es el auto más potente del
mundo.
![clip_image004[4] clip_image004[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiZ64p7AePWvc_Gu_6s1Qsn0iV6lgksnOtm7Wtunzyh44A32CTBVJHOAmCNgljLwtZJknC5e-mI5bpNCDm_BB0G71QzhP5LleNVA4Mdq9sEHnFScc9O6jvtzN3vMMUwa8BOkyl9O8QrcVpX/?imgmax=800) El
rubro de los súper autos está caliente, muy caliente. Luego de que el Hennessey
Venom rompiendo el récord mundial de velocidad y el Bugatti Veyron Se despachara
con sus 1,001CV, la batalla por tener el auto más potente más veloz se torna
cada vez más feroz (y más infantil), también.
El
rubro de los súper autos está caliente, muy caliente. Luego de que el Hennessey
Venom rompiendo el récord mundial de velocidad y el Bugatti Veyron Se despachara
con sus 1,001CV, la batalla por tener el auto más potente más veloz se torna
cada vez más feroz (y más infantil), también.
La marca sueca Koenigsegg Brindo los primeros detalles
de su nuevo deportivo llamado súper One:1. Según la empresa, El One:1 Eso es la
auto de producción más veloz del mundo Con sus 440 km/h Sí este dato parece
escalofriante, aún más escalofriantes es la relación entre potencia y peso del
auto. El modelo cuenta con un motor V8 de 5l que ofrece 1341 caballos de fuerza
y la misma cantidad de kilos. Es decir, un caballo de fuerza por
kilo.
Te preguntaras, ¿Qué es un caballo de potencia? La
siguiente figura muestra que un caballo de potencia (HP) equivale a mover un
objeto de 75 kg en 1 segundo.
![clip_image005[4] clip_image005[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjXd79rNsUTDFbzIl_FTPI9qUQ44yiO_fqtYCwYUvir6KccfIl6sphHQrG_3YOWgOxizuirSBw_qerMCgA7wVy7ZtdABoSQI-bDxAOR3usxNsBVrsG5DLyJUgbEzrfp4hVZziZ6s5mqKKNF/?imgmax=800)
La potencia es la “cantidad de trabajo
efectuado por unidad de tiempo”. Un enfoque constructivista. Todo el mundo ha
oído hablar de los “Caballos (CV)”
De potencia que tiene un coche. La gente ya sabe que un motor de 120
CV en un coche proporcionara más aceleración o más velocidad de subida en
una cuesta arriba que la que puede ofrecer un motor De 80
CV en un vehículo idéntico.
El primer problema aparece Al elegir las unidades con
la que se expresa la potencia.
Para el caso de la potencia, esta unidad es el vatio (W). El problema es que en la
industria automovilística tradicionalmente sea utilizado otra unidad: El caballo.
Así, se expresan y comparar las potencias de
automóviles, en caballos; y quizá no es habitual utilizar
vatios. El caballo cómo unidad
de medida presenta un problema adicional, no es único, Aunque muchas veces se
utiliza uno u otro de manera indistinta.
Los británicos en el siglo XVIII introdujeron el caballo de potencia (hp,
1 hp=746W), Y posteriormente los franceses introdujeron el caballo
de vapor (cv, 1cv = 735W). Dado que por lo general no hay grandes
diferencias entre utilizar unas u otras unidades, frecuentemente se comete el
error (o se realiza la aproximación) de trabajar indistintamente con HP o
CV.
Al regresar a los números que utilizamos antes esto se
expresan en las unidades del Sistema Internacional, por consiguiente, se
hablará de un motor de 80 CV = 58.8kW, O de un motor de 120 CV =
88.2kW.
Concepto de energía.
Hay otro concepto muy relacionado con el de potencia y
que también se ha estudiado: La energía. La energía se ha visto cómo “La
capacidad de realizar un trabajo”. Si se busca una explicación más intuitiva, el
concepto de energía se asimila aún “Almacén” qué va a proporcionar los recursos
necesarios para realizar un trabajo. En una marcha a pie, se recarga energía al
tomar alimentos Y nuestra reserva de energía estará determinada por el
contenido de nuestro almacén, es decir, por la cantidad de alimentos que se
llevan en la mochila. En un coche
con motor a combustión, la energía disponible vendrá determinada por los litros
de combustible contenidos en el depósito.
La unidad con la que se expresa la energía en el
Sistema Internacional es el julio o
Joules (J).
Sin embargo, hay otras muchas unidades equivalentes que se suelen utilizar al
trabajar en determinados contextos En el caso particular de referirse a energía
eléctrica se suelen utilizar el kilovatio-hora (kWh). Hay una relación
directa entre ambas, De tal modo que 1
kWh = 3,600,000J, o lo que es lo mismo,1kWh
= 3.6MJ.
El hecho de que aparezca “hora” en las unidades
proviene de la forma en la que se definen las unidades de energía. Así, un kWh Es la cantidad de energía
(Recordemos el concepto de almacén) para poder alimentar Durante 1 hora un
mecanismo (Por ejemplo, un motor) qué entrega una potencia de 1kW
(o, lo que es lo mismo, un motor de 1.36 CV). La cuestión es que esa
cantidad de energía no tiene por qué consumirse en 1 hora, aunque en el nombre
de sus unidades aparezca “hora”.
Es decir, sí el motor en lugar de tener una potencia de
1000 CV solo tuviera 500
CV, (o sea, la mitad) la reserva de energía duraría el doble de tiempo (es
decir, 2 horas). La comprobación es tan simple cómo multiplicar la potencia por
el tiempo:
![clip_image007[4] clip_image007[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgxU6_dfbWYLbpfmIYMEAUrKPlbdyp5VdKnlIXtXuv9bxgB5o71fJ0Sz49jJL-UhemRnxSkPrAVD_UgDv9SbYm9TcpytCxJZNU33NxnMmhKZ9uhXj2wufcXDNS5XYN3Q_iJva2N51BZORCx/?imgmax=800)
![clip_image009[4] clip_image009[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgz35F8F2PtXHDc8klaRvRNCdos2nlRE4rZaj5VNTJj0Ob1bAHVjjuLxGMk15bzxAmTtvMvpt4_Ry2J9dsZmnKumylEKsg8d9pbDqqCqalX6_jeAjokUY9ax7U8AVFpdWs-0zVWf1m9nn6K/?imgmax=800) Así
pues, con una energía de 1 kWh Se
podría alimentar un motor de 1000W
durante 1 hora, o se podría alimentar un motor de 200W
durante 5h, o se podría alimentar
un motor de 4kW durante 15 minutos
(0.25h). con lo que se puede concluir que la
energía es el resultado de multiplicar la potencia por el tiempo durante el
cual se entrega dicha potencia.
Así
pues, con una energía de 1 kWh Se
podría alimentar un motor de 1000W
durante 1 hora, o se podría alimentar un motor de 200W
durante 5h, o se podría alimentar
un motor de 4kW durante 15 minutos
(0.25h). con lo que se puede concluir que la
energía es el resultado de multiplicar la potencia por el tiempo durante el
cual se entrega dicha potencia.
Sería muy fácil evitar la confusión a la que en
ocasiones da lugar el concepto de energía simplemente utilizando la unidad del
Sistema Internacional (Julio o Joules). Así, por ejemplo, en lugar de
decir que la batería de un Nissan
Leaf puede almacenar 24 kWh de energía, se diría que puede Almacenar
86.4MegaJ (recuerda que 1kWh = 3.6MegaJ).
Entonces sustituyendo tenemos que:
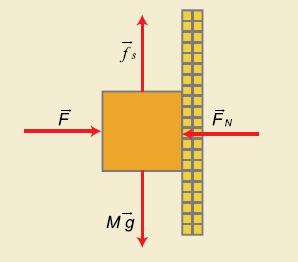
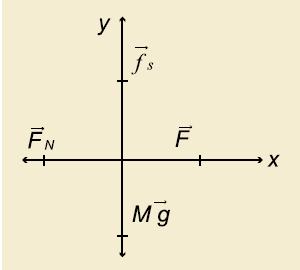
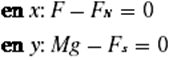
![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg5OvXtxRYoJ59ROLE_hIn4oeyMnrupCRD14r-p-lWiwEmM4ETKQ0OL5m04hiSWbrVWDKFX6ZBg0lMdDX0_ACTcJFNXBftJWnv9tfNeBC9JGu4DVW_DyE-HQgdNOwk7WohXcl3Sivjf70PE/?imgmax=800)
![clip_image004[4] clip_image004[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiZ64p7AePWvc_Gu_6s1Qsn0iV6lgksnOtm7Wtunzyh44A32CTBVJHOAmCNgljLwtZJknC5e-mI5bpNCDm_BB0G71QzhP5LleNVA4Mdq9sEHnFScc9O6jvtzN3vMMUwa8BOkyl9O8QrcVpX/?imgmax=800)
![clip_image005[4] clip_image005[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjXd79rNsUTDFbzIl_FTPI9qUQ44yiO_fqtYCwYUvir6KccfIl6sphHQrG_3YOWgOxizuirSBw_qerMCgA7wVy7ZtdABoSQI-bDxAOR3usxNsBVrsG5DLyJUgbEzrfp4hVZziZ6s5mqKKNF/?imgmax=800)
![clip_image009[4] clip_image009[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgz35F8F2PtXHDc8klaRvRNCdos2nlRE4rZaj5VNTJj0Ob1bAHVjjuLxGMk15bzxAmTtvMvpt4_Ry2J9dsZmnKumylEKsg8d9pbDqqCqalX6_jeAjokUY9ax7U8AVFpdWs-0zVWf1m9nn6K/?imgmax=800)









