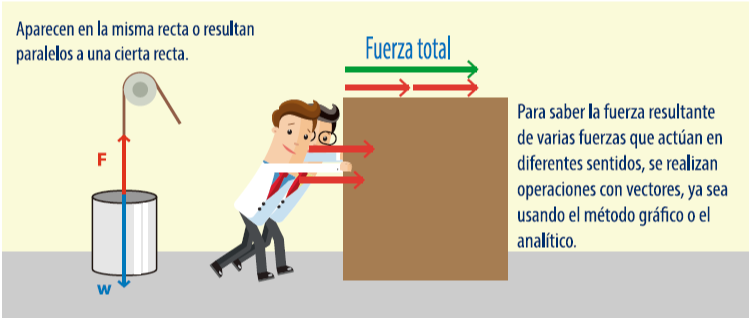
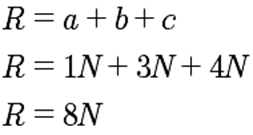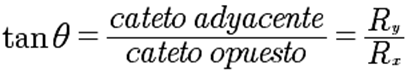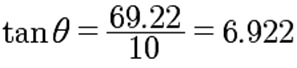Vectores colineales.
Los vectores
colineales, son aquellos que aparecen en la misma
recta o que resultan paralelos
a una cierta recta. Observa algunos ejemplos:
|
Método
|
Procedimiento
|
|
Gráfico de
suma de vectores colineales
|
Para sumar vectores colineales se deben trazar las
fuerzas de acuerdo con una escala (por ejemplo, 1N = 1cm), colocarlas de
acuerdo con su sentido (una después de otra) y medir la
resultante.
|
|
Gráfica de
resta de vectores colineales
|
Para restar vectores colineales se suman los vectores
y se trazan las fuerzas de acuerdo con una escala (por ejemplo, 1N = 1cm),
colocarlas de acuerdo con su sentido, las que tengan el mismo sentido una
después de otra y al final medir la resultante o diferencia entre
ellas.
|
|
Analítico
de suma de vectores colineales
|
Para este método se suman las magnitudes de las
fuerzas, debido a que todas van en el mismo sentido y
dirección.
|
|
Analítico
de resta de vectores colineales
|
Para este método se coloca un signo negativo a las
fuerzas que están en sentido contrario, ya que tienen la misma dirección, pero
en sentidos opuestos.
|
En algunas ocasiones se necesita saber la fuerza
resultante de varias fuerzas que actúan en diferentes sentidos. Para realizar
operaciones con vectores existen dos tipos de métodos: el método gráfico y el
analítico. A continuación, se describen como se realizan para los vectores
colineales.
Método gráfico: suma y resta de vectores colineales.
Los pasos generales para aplicar el método gráfico son:
seleccionar la escala adecuada y trazar los vectores con relación al sentido
que tengan.
Método gráfico: suma de vectores colineales.
A continuación, se resolverá un problema de suma que
involucra fuerzas colineales:
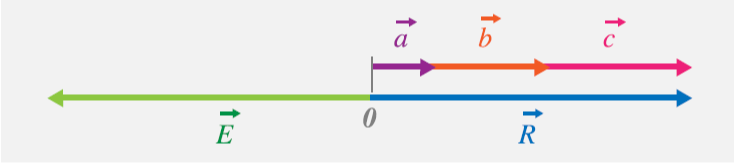
Cuál es la suma (resultante) de tres fuerzas colineales
de:
Observa que cada fuerza está representada con una letra
y con la flecha en la para superior que indica la dirección. De acuerdo con la
imagen, son tres personas las que aplican su fuerza para mover el auto en la
misma dirección. Cada persona aplica una fuerza diferente ¿Cuál será la fuerza
resultante?
Para encontrar la solución:
a) Elige
una escala para representar en papel milimétrico las cantidades de las fuerzas.
En este caso 1cm = 1N.
b) Dibuja
una recta y coloca la primera fuerza 1N
= 1cm, en la flecha de la primera coloca el origen y la segunda 3N
= 3cm y donde termina la segunda flecha coloca la tercera fuerza 4N
= 3cm. La distancia del origen de la primera fuerza hasta la flecha de la
última representara el valor de la resultante.
c) Como
se muestra en la siguiente imagen la resultante es
de:
Respuesta
La resultante del sistema R está dirigida
horizontalmente, en sentido hacia la derecha y tiene un valor numérico de R = 8N. el sistema de los vectores
dados puede ser sustituido por cualquier vector que cumpla con estos
requisitos.
La equilibrante
del sistema E está dirigida
horizontalmente, en sentido hacia la izquierda y tiene un valor numérico de E = -8N. El sistema de los vectores
dados puede ser equilibrado por cualquier vector que cumpla con estos
requisitos.
En resumen, para sumar vectores por el método gráfico
debes trazar las fuerzas de acuerdo con una escala (por ejemplo, 1N
= 1cm), colocarlas de acuerdo con su sentido (una después de otra como en el
ejemplo abordado), y al final medir la resultante.
Método gráfico: resta de vectores colineales
A continuación, se resolverá un problema de resta que
involucra fuerzas colineales:
Cuál es la resultante de:
Si a, b
tienen la misma dirección, pero c tiene sentido contrario de a
y b.
Para su solución se
necesita.
a) Elegir
una escala para representar en un papel milimétrico las cantidades de las
fuerzas. En este caso 1 cm =
1N.
b) Dibuja
una recta y en una línea todas las fuerzas que tengan el mismo sentido, donde
termina la flecha de la última, coloca el origen de la primera la cual está en
sentido contrario y donde termine la flecha, será el valor de la
resultante.
c) En
este caso la resultante es 0. Es
decir, si las fuerzas estuvieran moviendo un objeto, este se encontraría en
reposo pues las fuerzas aplicadas se anulan.
A manera de conclusión, para restar vectores, en el
método gráfico, debes trazar las fuerzas de acuerdo con una escala (por ejemplo,
1N = 1cm), colocarlas de acuerdo
con su sentido, las que tengan el mismo sentido, una tras de otra y al final
medir la resultante o diferencia entre ellas.
Método analítico: suma y resta de vectores colineales.
El método analítico no se dibujan los vectores porque
consiste en el uso de las propiedades matemáticas como la conmutativa para la
adición y la de negativo de un vector.
Método analítico: suma de vectores colineales.
Para este método, solo se suman las magnitudes de las
fuerzas, debido a que todas ven en el mismo sentido
y dirección. Así que para el caso anterior donde a
= 1N, b = 3 N y c = 4N, la
resultante (R) será igual
a:
Ahora se revisará la otra propiedad, la de la
resta.
Método analítico: resta de vectores colineales.
El método analítico, en el que las magnitudes de las
fuerzas solo se suman de manera aritmética, al colocar un signo de negativo a
las que están en sentido contrario, ya que tienen la misma dirección,
pero en sentido contrarios. Así para el caso anterior
donde:
La resultante (R), será igual
a:
Como puedes observar, para las operaciones con vectores
colineales el método gráfico requiere de instrumentos y materiales, en tanto
que el método analítico es solo la suma de sus magnitudes y la consideración
del sentido, lo que la hace más sencilla.
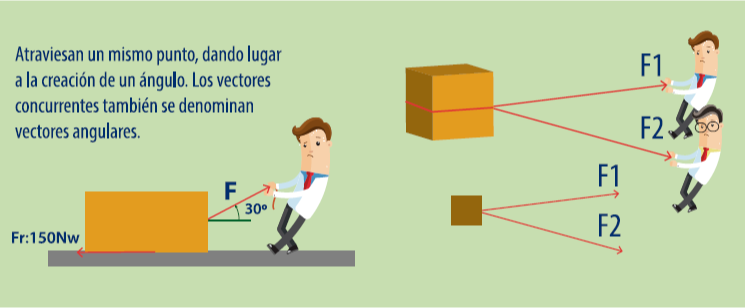
 Vectores
concurrentes.
Vectores
concurrentes.
Se llama vectores concurrentes a aquellos que
atraviesan un mismo punto. Debido a que, al pasar por dicho punto dan lugar a la
creación de un ángulo, los vectores concurrentes tambien se denominan vectores
angulares.
Método analítico: operaciones de vectores concurrentes.
El método analítico involucra operaciones con funciones
trigonométricas. A continuación, se abordará un ejemplo donde se obtendrá la
resultante de un sistema de fuerzas aplicadas a un
cuerpo.
Sobre un cuerpo se aplican diferentes tirones como se
muestra en la imagen, la acción de cada tirón se representa con el vector F. ¿hacia dónde se moverá el
cuerpo?

Análisis.
Para determinar hacia dónde se moverá el cuerpo, es
necesario calcular el valor numérico, la dirección y el sentido de la resultante
del sistema. puedes utilizar cualquiera de los métodos estudiados, pero por su
comodidad, se empleará el método de las componentes. Para auxiliarte, dibuja un
sistema de coordenadas rectangulares y en él, traza los vectores, haciendo
coincidir los orígenes de cada uno con el origen del sistema. Utiliza la escala
1cm = 10N.
Paso1.
Busca el valor de los componentes de los vectores
F1,
F2,
F3
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Paso2.
Encuentra los componentes del
vector.
Paso3.
Hallar el valor numérico de:
Paso4.
Para determinar el ángulo entre R
y el eje x, calcula la tangente del
ángulo .
Paso5.
Sustituye los valores:
Con una calculadora científica encuentra el valor del
ángulo correspondiente a esta tangente.
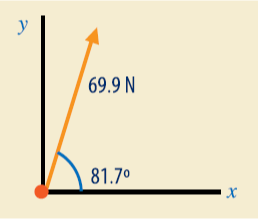
Paso6.
Con regla y transportador traza el
vector.
Utiliza como escala 1cm = 10N
Respuesta:
El vector suma tiene un valor numérico igual a R=69.9N y forma un ángulo de 81. 7º
con relación al eje positivo de las x.
El sistema se moverá a la derecha, la respuesta no es
exacta. En el problema no se considera el peso del cuerpo, vector que siempre
está dirigido hacia abajo, ni la resistencia del apoyo entre otras magnitudes
que varían las componentes de la resultante.
Es común que un cuerpo este siempre sometido a la
acción de dos o más fuerzas, por lo regular de tipo concurrentes que producen un
movimiento en los objetos, por lo tanto, es importante calcular la resultante
de esas fuerzas, con el propósito de interpretar y argumentar las
manifestaciones físicas que surgen en la naturaleza.