Teorema Fundamental del Cálculo.

La relación entre las derivadas y las integrales al momento no es del todo clara. Por un lado, las derivadas hacen referencia a la solución de un problema que consiste en hallar la pendiente de la recta tangente a una curva en un punto, en tanto que las integrales se enfocan en encontrar el área bajo una gráfica. Sin embargo, estas dos operaciones tienen una fuerte conexión, fueron Isaac Newton y Gottfried Leibniz quienes de manera independiente uno del otro estudió esta relación, y es enunciada como el Teorema Fundamental del Cálculo.

Primer Teorema Fundamental del Cálculo.

Si f es una función continua sobre el intervalo [a, b] y es una derivada de f en [a, b], entonces:

De esta manera, sabemos que con la antiderivada es posible calcular la integral definida y, por ejemplo, hallar el área bajo la gráfica de funciones de forma más sencilla.

Para usar este teorema basta con saber una antiderivada y evaluarla en los límites, la notación más común para este paso es la siguiente:

Observa que no es necesario agregar constantes de integración a F, puesto que al hacer la resta de los valores en a y b las constantes se eliminan.

En la ecuación del Primer Teorema Fundamental del Cálculo, en la que f(x)=F’(x), ya que es antiderivada de , se está integrando una función que es la derivada de otra. Para hacer la operación inversa sería necesario que la integral definida fuera una función (recordemos que es un número fijo). Para lograrlo, no se considera el valor del área desde hasta sino desde hasta un punto ∈ [, ]. El resultado de la operación de derivar esta nueva función definida a partir de una integral está enunciado en el siguiente teorema.

Segundo Teorema Fundamental de Calculo.

Si es continua en un intervalo abierto que contiene a , entonces, para todo en el intervalo:

En esta definición pueden verse dos variables x, t. La variable , la cual está dentro de la integral. Es decir, la variable de integración puede ser cambiada sin problema y no afecta el sentido de la función. A esto se le llama ser una variable muda. Lo que ocurre es que la variable t representa algo que se mueve en el intervalo [a, x]. Al integrar sobre ese intervalo, resulta un número, por lo que la función que se define por medio de la integral en realidad es una función y, por tanto, podría ser derivable.

Otro teorema que conviene mencionar es el Teorema del Cambio Neto, el cual es útil para determinar el cambio total a partir de la razón de cambio.

Teorema del Cambio Neto.

La integral definida de la razón de cambio de una cantidad F(x) proporciona el cambio total o cambio neto de esa cantidad sobre el intervalo [a, x]. En otras palabras:

Por ejemplo, cuando una partícula s se mueve s(t) representa la posición del tiempo t, su velocidad está dada por v(t)=s’(t); entonces, el cambio neto en posición de la partícula esta dado por:

Hasta aquí se ha dado una breve introducción a lo que son los teoremas fundamentales del cálculo. Se llaman así no porque sean totalmente indispensables siempre, sino porque de ellos se obtiene los principales resultados en la teoría del cálculo diferencial e integral.

Para aplicarlos de manera correcta en problemas reales, en general va a ser necesario obtener primitivas de funciones bastante complejas, por lo que será necesario aprender todos los métodos de integración. No obstante, un ejemplo sencillo a considerar es el del trabajo realizado por una fuerza al mover un objeto a cierta distancia, la cual se describe e a continuación.

Ejemplo 1 Cálculo del trabajo realizado por una fuerza. De cursos previos en secundaria, por ejemplo, se estudia que el trabajo que realiza una fuerza para mover un objeto en una cierta distancia puede determinarse simplemente multiplicando la fuerza por la distancia, es decir: Además, si la fuerza se dirige en sentido contrario a la del desplazamiento, entonces el trabajo es negativo; si es en el mismo sentido es positivo; y si la fuerza y el desplazamiento van en direcciones que son perpendiculares, entonces el trabajo que realiza esa fuerza es 0. En términos más generales, cuando la fuerza está en un ángulo que no es completamente horizontal o vertical, entonces el trabajo se define como: Comúnmente, estos planteamientos son correctos cuando la fuerza es constante, es decir, cuando la fuerza siempre es la misma sin importar la posición en la que se encuentre. También es posible que la fuerza cambie, dependiendo de la posición en la que esté el objeto. 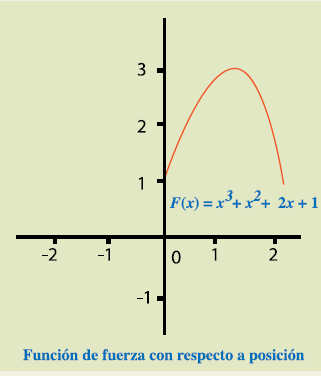Para considerar una función fácil de trabajar, supongamos que la fuerza cambia en cada punto de su recorrido debido a f(x)=-x3+x2+2x+1. Si se quiere calcular el trabajo que realiza esta fuerza para mover un objeto desde la posición 0 hasta la posición 2, es decir, una distancia de 2 unidades se debe calcular: En general, el trabajo que realiza una fuerza para desplazar un objeto del punto al punto se determina por: Se tiene, entonces, que el trabajo coincide con el área bajo la gráfica de la fuerza con respecto a su posición. Para este caso, se procede a integrar la función que define la fuerza en el intervalo [0, 2]: Dado que se deben las propiedades de la integral y se tiene una fórmula para integrar cada uno de los términos de la suma, así como por el Teorema Fundamental del Cálculo, la integral resulta: De esta manera, cuando la fuerza es constante y paralela al desplazamiento, calculamos solo el área de un rectángulo. De ahí que la formula sea: w = F • d

La integral ha sido presentada de las dos formas principales como operación inversa de la derivada y a partir de la generación de la noción de área bajo la gráfica, así como también la relación entre derivada e integral a través de los teoremas fundamentales del cálculo.

Este es solo el inicio, por lo que es necesario dominar los razonamientos que se usaron en estos temas para desarrollar más herramientas que permitan el estudio de problemas cada vez más complejos. La matemática es una ciencia en desarrollo, así que también existen conceptos aún más abstractos y que requieren mucho estudio y, para nuestro propósito, el cálculo es solo el inicio de este fabuloso mundo matemático.