Al calcular la derivada de una función se obtiene otra función con características diferentes, pero que reflejan el comportamiento de la función original. Vale la pena preguntar si es posible, teniendo la derivada, saber la función de la que provino. Esta pregunta la resolveremos dentro del tema que estudiaremos a continuación.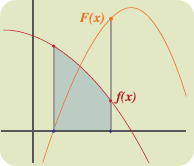

Considera, por ejemplo, la función F cuya derivada es f(x)=3x2. La función puede ser F=x3 ya que d/dx[x3]=3x2. Sin embargo no es la única función que cumple con que su derivada es f, pues la función x3+3 tiene la misma derivada. De hecho, existe toda una familia de funciones que cumplen con esa propiedad y solo difieren en la constante que se les sume o reste, ya que la derivada de una constante siempre es cero.
Se define F como la antiderivada, a veces la llamada primitiva, de una función f en un intervalo I, es decir como una función tal que para todos xεI se tiene que f’(x)=f(x).
Si se sabe que F es una antiderivada de la función f en el intervalo I, entonces todas las demás antiderivadas difieren de F en una constante, es decir, si:
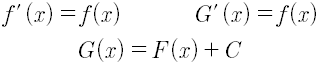 Donde C es una constante cualquiera, que es llamada la constante de integración. Así, cuando se habla de la antiderivada se suele mostrar toda la familia de antiderivadas mediante un representante y agregando la constante de integración.
Donde C es una constante cualquiera, que es llamada la constante de integración. Así, cuando se habla de la antiderivada se suele mostrar toda la familia de antiderivadas mediante un representante y agregando la constante de integración.
Al proceso de obtener la antiderivada también se le conoce como integración indefinida, y es denotado por el símbolo ∫. La idea detrás de este símbolo es que representa una mayúscula alargada que en su historia la antiderivada o integral surge como un proceso límite de sumas, dando como resultado sumas de cantidades continuas. De esta manera, la notación que se usa para expresar las antiderivadas es como sigue: Si ’()=() se escribe la familia de antiderivadas o la integral indefinida como:
Donde ƒ es el integrando o función a integrar, x es la variable de integración, F una
antiderivada conocida de ƒ y C la constante de integración.
La expresión completa se lee como la primitiva o integral de ƒ con respecto
a x. Dentro de ésta se puede notar el término dx, el cual indica a la variable
independiente.
|
Para comprender mejor como se trabajan las
antiderivadas puedes pensar en su importancia. En la naturaleza existen muchos
fenómenos físicos y es de interés para los científicos investigar si estos
procesos siguen algún comportamiento determinado y se pueden reproducir o
pronosticar.
A través de la historia muchos científicos han podido
establecer estas leyes y comportamientos, permitiendo traducirlos a un lenguaje
preciso y claro. Este lenguaje es el matemático. Los avances más grandes de la
humanidad se han logrado gracias al descubrimiento de las leyes que siguen los
fenómenos físicos. Los ejemplos clásicos son las leyes del movimiento, de la
gravedad, de las cargas, de la fuerza, entre otras. Es posible que conozcas
planteamientos referidos a estos temas que no mencionen ecuaciones matemáticas
en sí, sin embargo, es común que se vean versiones simplificadas para
divulgación; es decir, hay muchas más teorías detrás de
ellas.
Lo importante en la práctica de las derivadas es que
muchas de las leyes físicas hacen uso de ellas. Ya viste que la derivada de la
posición respecto del tiempo es la velocidad. Este es un ejemplo claro de lo
dicho.
|
En la realidad, es posible obtener mediciones parciales
de un fenómeno. Por ejemplo, es posible determinar la velocidad, pero nos parece
necesario obtener la posición del objeto en un cierto momento que cumplo con esa
velocidad. Entonces, la incógnita es la función y lo que se sabe es la derivada.
A este tipo de ecuaciones se les denomina ecuación diferencial.
En general, una ecuación
diferencia en x
y y
es una ecuación que incluye a x, y y a las derivadas de y, por ejemplo y=y, y’=x+y. Claro, las de mayor
importancia son las que se relacionan a fenómenos
físicos.
Si se quiere resolver estas ecuaciones diferenciales es
posible hacerlo mediante el proceso inverso de derivación, el cual es similar en
tanto se aplican las operaciones inversas; es decir, se debe integrar.
Usualmente, las ecuaciones son muy complejas y requieren de métodos más
complicados para encontrar la solución analítica, en el entendido de que la
solución solamente es una aproximación.
|
Ejemplo
2.1
Solución
de una ecuación diferencial
Considera la ecuación y´=
2x. Para resolverla, recordemos que la función
y´=
x2 tiene como derivada 2x, entonces todas las posibles soluciones deben ser
y´=
x2 +
C. Como podrás comprobar, éstas son
parábolas.
|
La
siguiente tabla resume las principales fórmulas de derivación e
integración:
|
Fórmulas de
derivación
|
Fórmulas de
integración
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Puedes notar que no se hace referencia a la integración
del producto de funciones porque requiere de otro procedimiento y métodos
especiales. Esos métodos son:
· Cambio de
variable.
· Integración por
partes
· Descomposición en
sumas parciales.
|
Ejemplo
2.2
Integral
de funciones
Puedes notar que la constante aparece en cada una de
las integraciones. La constante también puede ir multiplicada o dividida, sin
embargo, es mejor mantener todo en una sola constante C.
|
Como ya se mencionó, al obtener la integral de una
función se obtienen una familia de soluciones. Cuando se busca resolver un
problema se espera que tenga una solución única, pero no siempre es posible.
Existen problemas conocidos como “mal planteados”, los cuales tienen varias
soluciones. En algunas de las aplicaciones de integración se busca tener una solución particular, por ello se
requiere que más información que lleve a la determinación del elemento de la
familia de soluciones. La
información necesaria es conocida como condición inicial, y se refiere al
valor de la función en algún punto dentro de su dominio. Usualmente se usa el
inicio del intervalo, de ahí que se llame inicial.
En el siguiente ejemplo se ilustra la manera de obtener
una solución particular a una ecuación diferencial muy sencilla relacionada con
la función exponencial, dándole una condición inicial
especifica.
|
Ejemplo
2.3
Solución
particular
Encontrar
la solución a la ecuación diferencial y´= ex,
con
condiciones iniciales y (0) = 2.
Por la
Tabla 2, se sabe que la solución general es:
Usando la
condición inicial y
(0)
= 2, basta con sustituir el valor de
x
y
despejar la constante C:
De esta
manera, la solución particular que se busca es y(x) = ex
+
1.
|
La ecuación diferencial parece ser muy sencilla, sin
embargo, es de gran utilidad ya que la función exponencial aparece en varias
leyes de gran importancia de la física, entre las que se pueden mencionar son
las leyes de decaimiento radiactivo, crecimiento de una población en tiempos
pequeños y caída libre en aire, entre otros.
El siguiente ejemplo muestra el procedimiento a seguir
usando la antiderivada para resolver un problema relacionado con la velocidad y
la aceleración. Recuerda que la velocidad es la primera derivada y la
aceleración la segunda.
|
Ejemplo
2.4
Gravedad
lunar
Se sabe
que sobre la luna la aceleración de la gravedad es de
-1.6
mm/s2.
Si
en este medio cae una roca desde un peñasco y golpea la superficie de la luna,
y el tiempo fue de 20 segundos ¿de qué altura cayó la roca? ¿Cuál era su
velocidad en el momento del impacto?
Solución
Denotando
s
(t)
la
posición del objeto en términos del tiempo, lo que se busca es la altura
inicial s
(0),
sabiendo que s
(20) = 0. Como la roca cae, si velocidad inicial es de
s’
(0) = 0 y que s” (t) = −1.6, integrando se tiene
que:
Sabiendo
la velocidad inicial s’
(0) = 0 = −1.6(0) + C, se
obtiene el valor de C1
=
0.
Ahora integrando s’
(t), se obtiene el valor de la altura en función del
tiempo:
Usando la
última condición inicial s (20) =0=-0.8(20)2+C2=-320+C2,
la función que da la altura con el
tiempo es s(t)=-0.8t2+320.
Sabiendo este dato, la altura de la que cayó la roca es s
(0) =320 metros y la velocidad con la que toco el suelo fue de s’ (20)
=-1.6(20) =-32m/s
|
Existen muchas ecuaciones que modelan distintos
procesos y fenómenos. Dependiendo del contexto, las derivadas tienen
significados diferentes, pero el punto de partida es siempre el cambio
instantáneo de una variable con respecto de otra. De ahí la importancia del
estudio de razones de cambio.
Las antiderivadas, hasta cierto punto son la operación
inversa de las derivadas. Sin embargo, en su inicio fueron obtenidas de un
proceso independiente al estudiar un problema relacionado con la generalización
del área de las figuras planas ya conocidas (como el cuadrado, el circulo, el
triángulo, etc.) a regiones que estaban delimitadas por la gráfica de una
función. La obtención de las integrales definidas por este proceso es descrita
en el siguiente subtema.
Aplicación de la integral. Área bajo la gráfica de una función.
Cuando
se tiene una función continua definida en un intervalo [a,
b] se puede considerar encerrada el área por el eje x.
la gráfica de la función y las rectas x=a, x=b, en la siguiente figura, son
ejemplos de estas regiones. Observa que es posible que el área esté bajo el eje
x, esto suele interpretarse como
área con signo, es decir puede haber áreas negativas. Si se requiere saber el
área sin signo, basta con tomar el valor absoluto del área que es negativa y
sumar el área positiva.
![clip_image002[17] clip_image002[17]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEimjcBTlDEGAYG04FCcVB5E0jfg_yMp727v951TZzvx2zjX8c06YgDC9KcIHn_x9TW49bE7-qbUFpjSUCA8PARZfBPCgGgPc0K5rLv1K0saUcaHXiOQNqCmAWDlJ5gTHaiAuZbY7F70FR7k/?imgmax=800) para
calcular el área de este tipo de regiones puede aplicarse un método de
estimación que consisten aproximar el área que se quiere por rectángulos, con
base sobre el eje x y como altura
un punto sobre la gráfica.
para
calcular el área de este tipo de regiones puede aplicarse un método de
estimación que consisten aproximar el área que se quiere por rectángulos, con
base sobre el eje x y como altura
un punto sobre la gráfica.
La figura de la derecha muestra la construcción de esos
rectángulos. Conforme la base de los rectángulos se hace más pequeña, el número
de estos aumenta, pero la suma de todas las áreas se acerca cada vez más a la
deseada.
Para construir estos rectángulos de una función f en un intervalo [a,
b] el primer paso es considerar una partición de puntos de este intervalo,
es decir n+1 puntos, denotados
xi [a,
b], de manera que a=x0<x1<x2<…<xn-1<xn=b. la manera
usual para tomarlos es considerando un incremento:
Y tomando xi=a+iΔx.
Con esto se consiguen puntos igualmente espaciados o una partición
homogénea.
Entonces, la base de los rectángulos que se usarán para
aproximar el área será Δx.
Ahora, la altura varia, en cada intervalo se considera un representante. Se
necesitan n puntos, uno en cada
subintervalo. Es decir, se necesita Ci
[xi-1,
xi],
i=1, …, n, y la altura que se tomará
será f(Ci). existen
muchas maneras de considerar estas alturas, lo que genera diferentes tipos de lo
que se conoce como “sumas”. Si se escogen los máximos y mínimos de los valores
en el intervalo se llaman “sumas de Darboux”. Si son extremos de los intervalos,
suelen llamarse sumas derechas o izquierdas, según sea el extremo que se usó, y
así toman un punto cualquiera sin algo en especial son “sumas de
Riemann”.
|
Nota.
para construir rectángulos es necesario tener n+1 puntos, pues se empieza a contar
desde 0 y se termina en el extremo
b, en el punto xn.
|
Para finalizar la aproximación basta con sumar las
áreas de todos los rectángulos. En general, puede escribirse para una función f continua en el intervalo [a,
b]. la región bajo la gráfica de la función llamada en este caso R
se aproxima:
Para facilitar los cálculos en los ejemplos se toman
sumas laterales, pero puede hacerse uso de cualquier tipo de sumas; las más
usadas en niveles superiores para trabajar el área bajo la curva son las de
Darboux. Puesto que existe un orden en los valores que resultan si se aumentan
los puntos a una partición dada, cosa que no ocurre en una suma lateral, por
ejemplo.
Cuando el número de puntos de la partición aumenta, la
aproximación del área que se necesita es cada vez mejor, esto siempre que la
función sea continua o con pocos puntos donde sea discontinua en el límite,
ambas cantidades coinciden. De esta manera se define el área de la región R bajo la gráfica de la función
continua f en el intervalo [a, b] por:
Se analizará el paso al límite en el ejemplo 2.1.1.
para calcular el área de la región señalada.
|
Ejemplo.
2.1.2
Cálculo
del área de una región bajo la gráfica de una función.
De acuerdo
con el ejemplo anterior, se tenía la función ƒ(x)
= x2 sobre el intervalo [0,
2],
y se quiere determinar el área bajo la gráfica de la función, por lo que es
necesario calcular el límite:
Para
empezar, se considera un número n
arbitrario, pero de momento fijo; es decir, no lo cambiaremos hasta tener el
valor de la suma, con esos n
intervalos. Basados en los cálculos hechos ya en el ejemplo 2.1.1 se tiene
que:
Entonces la suma tiene la
forma:
Cuando se hace el paso al límite, se calcula la última
expresión como ya se conoce:
Entonces el área de la región
es:
|
Lo que se ha dicho hasta ahora es siempre verdad cuando
la función es continua, pero existen funciones que no son continuas a las que es
posible calcular el valor del área de la región que denotamos R.
sin embargo, no es útil tomar una partición homogénea, sino que debe ser más
general. Es decir, Δxi=xi-xi-1 puede ser diferente para cada i.
ese tipo de sumas se denominan “sumas de Riemann” e incluyen a los elementos que
son sumas con particiones homogéneas. En general, es usada la definición de
Riemann para establecer el área bajo la gráfica de una función, como se enuncia
a continuación:
|
Si
es una función sobre el intervalo [a,
b]
y
el límite sobre las particiones P
|
Entonces f
es integrable según Riemann (o Riemann integrable) en a,
b y el limite se denota por:
Este límite recibe el nombre de integral definida de f en [a,
b].
Cuando existe este límite es uno de los primeros
problemas que se pueden tener, pero existe un teorema que asegura que si la
función es continua en [a, b]
entonces es integrable, según Riemann. Debe quedar claro que el converso no es
cierto, es decir, existen funciones integrables que no son
continuas.
Como se dijo en un inicio, el símbolo de integrar
parece surgir con el paso al límite de la letra Sigma (Σ)
así como el cambio Δxi se
vuelve. Adicionalmente, se debe subrayar que la notación es extremadamente
similar a la antiderivada o integral indefinida, por lo que se debe señalar que
no son lo mismo. De hecho, la integral indefinida, por lo que se debe señalar no
son lo mismo. De hecho, la integral indefinida es una familia de funciones y la
integral definida es un número. Sin embargo, como la notación ya lo sugiere,
debe haber cierta relación entre ellas. Esa relación se marca claramente en el
Teorema Fundamental del Cálculo.
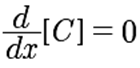
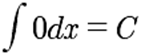


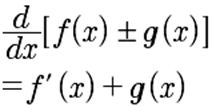






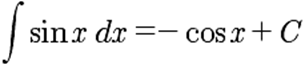
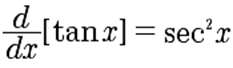
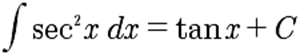










![clip_image004[7] clip_image004[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgcXcvEdzKRsYtV5x85ahXFkR5xpEUz-jGlqkYYjBJ7lBVZ81U1092JEAsVs5DhcrP0mu7SgnqowkWsoT-iTloLBs8sqbKk1eDF0vpas2Y2jJwQ8imkTz9TL8CpMjhwtIRWguFYesQMoseR/?imgmax=800)
![clip_image006[8] clip_image006[8]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiMWglW1ymr5gg3NSHqw3zZFe5SbMpM6oX2ev4qXL40ytSNgInKr7zjPGrqHgulWpTmDhL6VCKioHJtOFazxDVp7T6gnS0-S-A0V_UF05OMsjbdwxzjRFPStT9_-YrAdk1vHiPqX9ke53ga/?imgmax=800)
![clip_image008[9] clip_image008[9]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhUanOP-Ph7WsyhipbVFwja8HO0eStfw4u6BOg78gppi2EApjFA2AZIbUyzg4yqkQAcP1adAkWMDX167eIlIHDtiCcKWlFxfplQP8Dm6ih9uoqTkpTH5DDe9Ah19Cy-Uffr6qou8LYM6yn0/?imgmax=800)
![clip_image010[7] clip_image010[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhuy98_dJ4J7vtlr6cEei-uOGABieCkXrlqVfI4OjUQrEk1WE3HQ09WXmQQyCNOX275bFK8D117cV85lPzNCBYAsc-P622cVpxeb127eaOz7OG86e3Z78fhYRt9tlx2eosffD984q8AczBA/?imgmax=800)



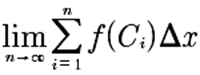









No hay comentarios.:
Publicar un comentario