Funciones logarítmicas.

Las funciones logarítmicas y las funciones exponenciales se encuentran relacionadas estrechamente pues una en inversa de la otra. Es decir, la potenciación y el cálculo de logaritmos, entendidas como operaciones son opuestas tal como la multiplicación y división, o bien, como la adición y la sustracción.

Recuerda que la potenciación se define de la siguiente forma:

                                                                        

La potencia k de un número a es b. Dicho de otra forma, a elevado a la k como resultado el número b.

Con base en lo anterior, el logaritmo se define de la siguiente forma:

La expresión anterior se lee como sigue: el logaritmo base a del número es igual a k. Por lo tanto, el logaritmo permite obtener el exponente al que se tiene que elevar una base a para obtener el número b. Cabe mencionar que existe en la definición una restricción para la base a. Para que un logaritmo pueda existir, debe cumplirse que la base del logaritmo sea positiva y que no sea uno, es decir: a>0 y a≠1.

Consideremos las siguientes operaciones:

a)       Log₂(16) = 4 porque 2⁴ = 16

b)      Log₅(125) = 3 porque 3⁵ = 125

c)       Log₁₀(1,000,000) = 6 porque 10⁶ = 1,000,000

Con estos ejemplos puede verse claro porque siempre se dice que el logaritmo y la potencia son operaciones inversas. Como se mencionó antes, el logaritmo es el exponente al que hay que elevar una base para obtener cierto número.

Existen dos logaritmos que son muy especiales. El logaritmo de base 10 y el logaritmo de base e. El logaritmo de base 10 suele escribirse sin la base, es decir: log₁₀(x)=log(x).

Y el logaritmo de base y suele ser llamado logaritmo natural o logaritmo neperiano y se escribe:

Debido a la relación inversa entre las potencias y los logaritmos, estos últimos son muy útiles para resolver problemas que involucran crecimientos exponenciales.

Propiedades de los logaritmos.

En términos generales, los logaritmos cumplen con las siguientes propiedades, las cuales resultan evidentes por estar relacionadas con la potenciación:

A continuación, veremos la utilidad de los logaritmos para resolver algunos tipos de problemas.

El Carbono-14 (¹⁴C) es un isótopo radioactivo del carbono que está presente en todos los materiales orgánicos, por lo que es empleado para la datación de especímenes orgánicos.

El método de datación por Carbono-14 es la técnica basada en isótopos más fiable para conocer la edad de muestras orgánicas de menos de 45000 años y está basado en la ley de decaimiento exponencial de los isotopos radiactivos.

Por ejemplo, es posible bajo esta técnica determinar la edad de algún material orgánico con base en la siguiente expresión matemática, la cual representa un comportamiento exponencial de decaimiento, como los que se han mencionado en el apartado anterior:

Donde C₀ representa la cantidad actual de ¹⁴C en la atmósfera, C el porcentaje de ¹⁴C que presenta el fósil y el número -0.00012378 representa el factor que en cada periodo reduce la cantidad de ¹⁴C, es decir, el factor de decaimiento.

En general, esta expresión permite calcular la cantidad de ¹⁴C que tiene un material orgánico para cualquier tipo, puesto que la expresión tiene como variable el tiempo. Por consiguiente, es posible calcular también el tiempo (la edad) si se realizan algunas operaciones sobre la expresión.

Por ejemplo, supongamos que se quisiera determinar cuál es la edad de un fósil que actualmente presenta un 5% de ¹⁴C.

è Debido a que se sabe que el fósil presenta un 5% de ¹⁴C con respecto a la cantidad que hay en la atmósfera, entonces se cumple que C=0.0C₀. Por lo que tenemos que:

è En los siguientes pasos es donde cobran un papel esencial los logaritmos pues son fundamentales para resolver problemas de tipo exponencial en los que interesa determinar el valor del exponente en la expresión. En el caso del ejemplo, interesa determinar el exponente, el cual representa la edad del fósil.

Para resolver entonces la ecuación, hay que despejar la variable t. Primero C₀ que está multiplicando se pasara dividiendo y se cancelara:

è Para despejar t, se obtienen logaritmos a ambos lados de la ecuación para no alterarla y dado que la base de la potencia es e, entonces se usará el algoritmo natural. Así:

è Debido a que se base que el fósil presenta un 5% de ¹⁴C con respecto a la cantidad que hay en la atmósfera. Por lo tanto, tenemos que:

Recordando que el log_abⁿ=n·log_a (propiedad 5) se obtiene que:

Y considerando también que:

Despejando se obtiene:

è Por lo tanto, realizando los cálculos se tiene que:

Esto quiere decir que el fósil tiene aproximadamente 24,202 años.

Esta técnica ha sido muy empleada por historiadores y arqueólogos desde hace años atrás y mucha de la información en cuanto a la edad de los materiales orgánicos que hoy en día conocemos se debe a la misma, en la cual el logaritmo juega un papel fundamental.

 

Funciones logarítmicas.

Como ya hemos visto con anterioridad las gráficas de las funciones exponenciales, ahora veremos la gráfica de las funciones logarítmicas. Para ello recurramos a la técnica de la tabulación.

Para valores de x mayores que uno:
x		y
1	Log (1)	0
2	Log (2)	0.30103
3	Log (3)	0.47712125
4	Log (4)	0.30205999
5	Log (5)	0.69897
6	Log (6)	0.77815125
7	Log (7)	0.84509804
8	Log (8)	0.90308999
9	Log (9)	0.95424251

Para valores de x entre 0 y 1:
x		y
0.1	Log (0.1)	-1
0.2	Log (0.2)	-0.69897
0.3	Log (0.3)	-0.52287875
0.4	Log (0.4)	-0.39794001
0.5	Log (0.5)	-0.30103
0.6	Log (0.6)	-0.22184875
0.7	Log (0.7)	-0.15490196
0.8	Log (0.8)	-0.09691001
0.9	Log (0.9)	-0.04575749

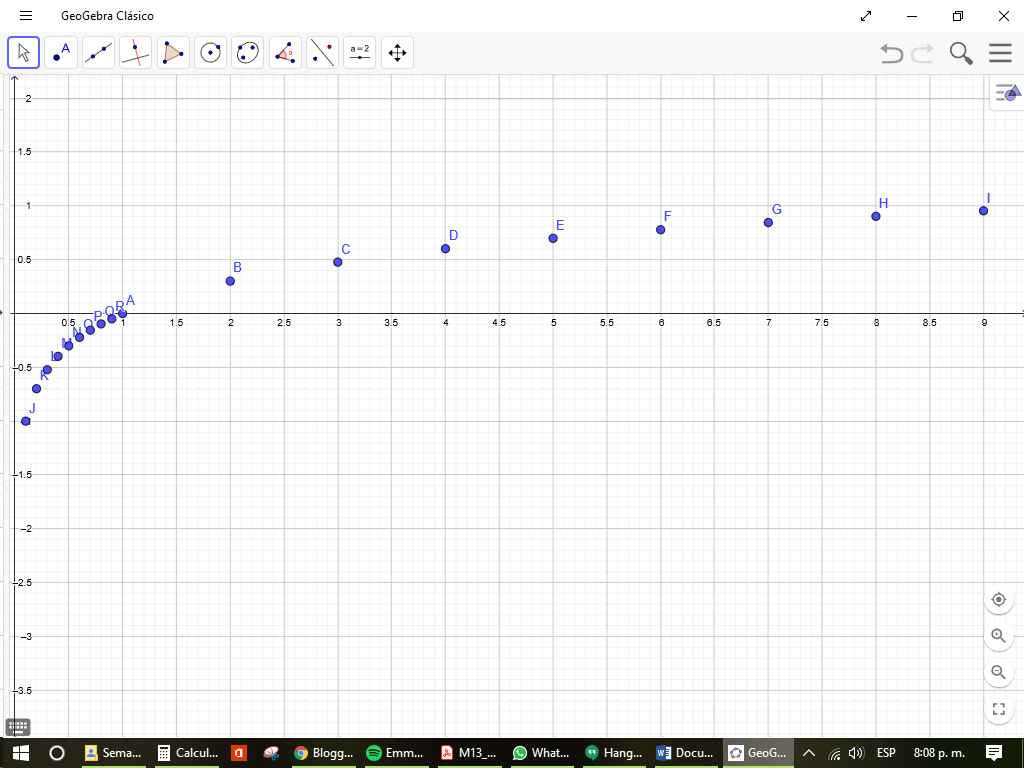
Por lo tanto, con los pares encontrados, la gráfica se ve de la siguiente forma:

De forma completa, considerando valores de x mayores que cero se obtiene que la gráfica de una función logaritmo es la siguiente:

Como puede observarse, no hay curva para valores menores o iguales a cero puesto que la base del logaritmo no puede ser cero o un número negativo por definición. Además, para valores de 0 y 1 el crecimiento de la gráfica es rápido, en tanto que para valores mayores que uno el crecimiento es mucho más lento en comparación.