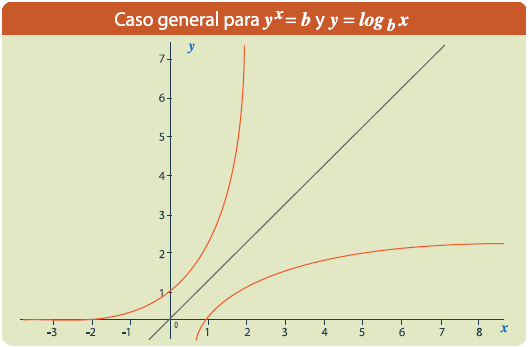
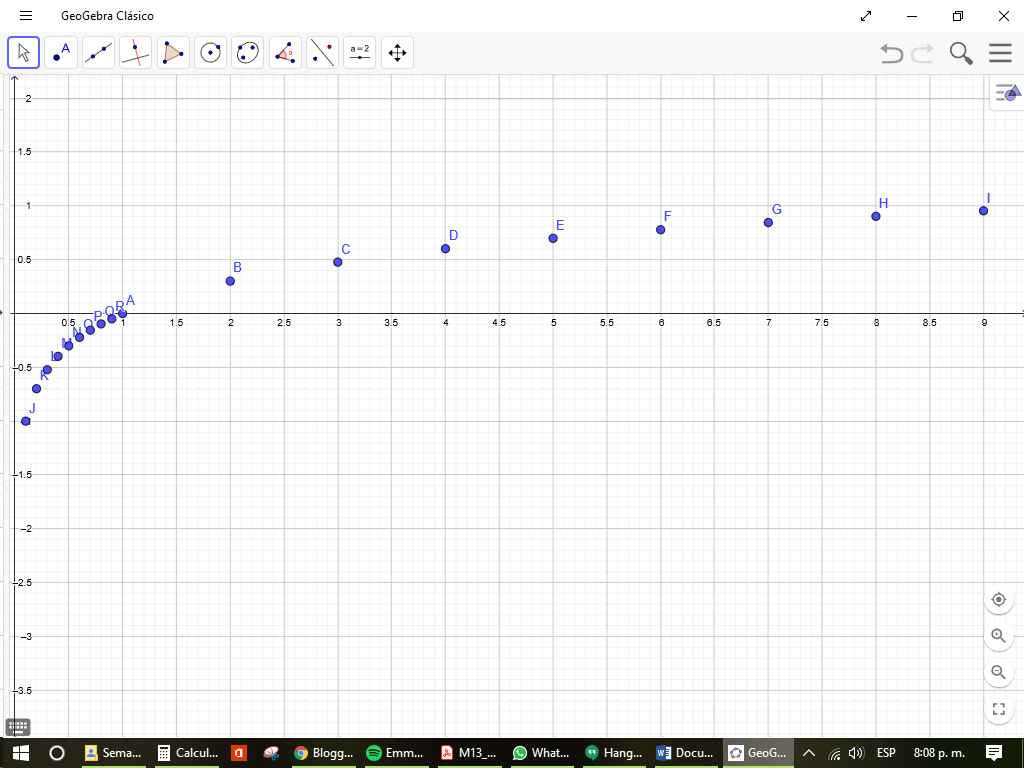
Una función se llama logarítmica cuando es de la forma y = logax donde la base es un numero real y positivo distinto de 1. El tema se explicara mediante un ejemplo: Un terremoto tambien es llamado seísmo o sismo, o simplemente, temblor de tierra, y es posible medir su magnitud y su intensidad. Para ello, se utilizan varias escalas; las mas comunes las mas comunes son la de Richter y la de Mercalli.
- Richter mide la magnitud = Causa
- Mercalli mide la intensidad = Efecto.
La escala Richter, es una escala logarítmica que corresponde a la medida de las ondas de tipo P y S tomadas a 100 kilómetros del epicentro.
La formula para calcular la escala de Richter utiliza un logaritmo decimal: ML= logA-logA0’ donde A representa la amplitud máxima revelada por el sismógrafo A0 y una amplitud de referencia. Estos significa que las ondas sísmicas de un temblor de magnitud 6 tienen una amplitud diez veces mas grandes que aquellas de uno de magnitud 5.
Richter se inspiro en la escala de magnitud estelar. Esta es una técnica usada en la astronomía para describir el brillo de las estrellas y de otros objetos celestiales.
En la escala de Richter se establecen las siguientes categorías de un sismo:
|
Intensidad |
Descripción |
|
Menos de 3.5 |
Generalmente no se siente, pero es registrado |
|
3.5 – 5.4 |
A menudo se siente, pero solo causa daños menores |
|
5.5 – 6.0 |
Ocasión daños ligeros a edificios |
|
6.1 – 6.9 |
Puede ocasionar daños severos áreas muy pobladas |
|
7.0 – 7.9 |
Terremoto mayor. Causa graves daños |
|
8 o mayor |
Gran terremoto. Destrucción total a comunidades cercanas |
Para medir la magnitud de un sismo se realizan lecturas en un sismógrafo, las que están representadas en una escala. En 1935, Charles Richter definió la magnitud de un terremoto como:
El 31 de mayo de 1970 un terremoto asolo el Callejo de Huaylas (Perú) durante 45 segundos, el cual causo la destrucción de las principales ciudades y ocasiono aproximadamente 67,000 victimas.
Si a 100 Km del epicentro hubiera estado ubicado un sismógrafo, este habría registrado una lectura de 31,622.77mm. Ahora puedes determinar la magnitud del sismo.
Yodos los sismos se compara con uno de nivel cero, cuya lectura sismográfica mide un milésimo de milímetro a una distancia de 10Km del epicentro.
La magnitud de este terremoto es de 7.5 escala de Richter.
Los astrónomos que determinan una magnitud estelar de una estrella o planeta, realizan ciertos cálculos del logaritmo. La función logarítmica les permite determinar cuales son las mas brillantes.
La función logarítmica de base b es la inversa de la función logarítmica de la base b es la inversa de la función exponencial de la base b.
Se usara la notación f(x)=logb o f(x)=logbx, la cual se lee como logaritmo de base b de x. Por consiguiente, y puesto que logbx y la función exponencial:
y = logb x si y solo si x = by
En los siguientes ejemplos se muestra como se puede aprovechar este razonamiento:
En los siguientes ejemplos se explica el método para obtener los valores de los siguientes logaritmos:
- log7 49 = y
Esta ecuación es equivalente a 7y = 49,
ya que: 49 = 72 ,
se tiene: 7y = 72,
por consiguiente: y = 2;
esto es: log7 49 = 2
- Se toma: log5√5 = y,
por esta razón: 5y = √5,
o bien equivalentemente: 5y = 51/2
entonces: y = 1/2;
es decir: log5√5 = 1/2 cc
Al recordar los ejemplos anteriores, el log puede tener distintas bases. Las bases mas usadas son la decimal y la exponencial. Incluso, es tan usada la base decimas que es común no indicarla, esto es:
En tanto que el logaritmo con base se denota comúnmente con ƒ(x ) = In x
De lo anterior se puede hacer el siguiente resumen. La exponencial, la función logarítmica, se usa de manera frecuente en los cálculos y las matemáticas, asi como en las ciencias naturales y las ciencias sociales, como en el ejemplo que muestra la forma en que se calcula la intensidad de los terremotos. Por esta razón, se debe tomar en cuenta que la función tiene gran cantidad de propiedades explicativas.
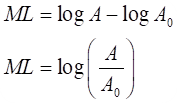
![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjOlYAGXkmW8Y61EQXFrvQDbC8j3OiKNsUGF1WoWZ3i6QVc93mzkU6ory2tGffp4vvDtW0hqqHpE3HWsgJAASrl7S3Xx-TJOMCAL35P4kq1ZhC7btopmea1MvwmD9C1fENSa5H4cq8KIXYe/?imgmax=800)