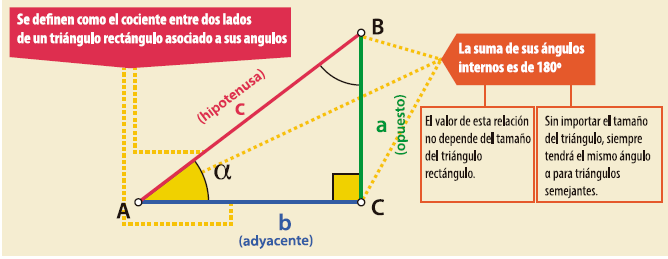
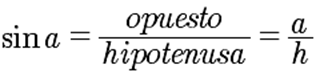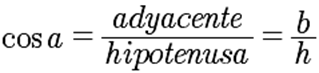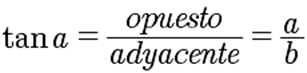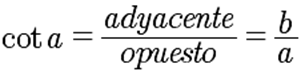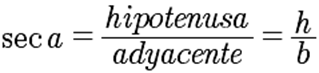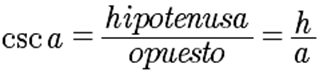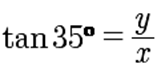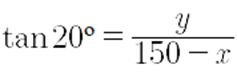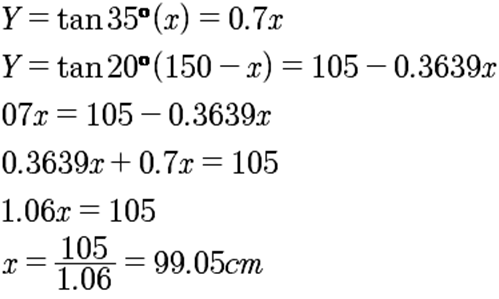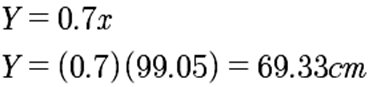Las razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. La suma de los ángulos internos es de 180° y el valor de esta relación no depende del tamaño del triángulo rectángulo elegido, siempre tendrá el mismo ángulo (α), en cuyo caso se trata de triángulos semejantes.
A continuación, se presenta una tabla que contienen las razones que existen entre los lados y los ángulos de las figuras anteriores de los triángulos rectángulos, con referencia al ángulo alfa (α).
Razones entre los lados y ángulos con referencia al ángulo Alfa(α).
|
El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa |
|
|
El coseno de un ángulo, la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa |
|
|
La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente |
|
|
La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto |
|
|
La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente |
|
|
La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto |
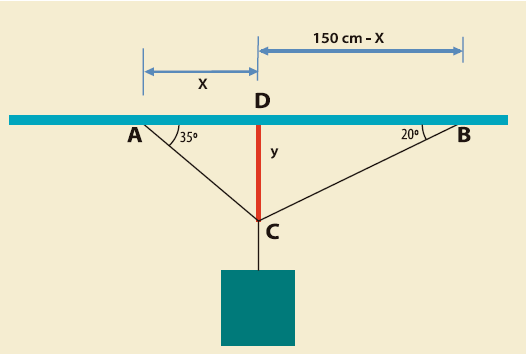
En las siguientes figuras se observó un objeto que está soportado por dos cables sujetos en el derecho de los puntos A y B. Se necesita calcular la distancia que existe entre C y D, para conocer esta distancia, se usarán las razones trigonométricas.
Para calcular la distancia que hay entre el pecho y el objeto se han medido los ángulos de los extremos.
La distancia es la altura del triángulo ACB Qué no es un triángulo rectángulo, pero sí lo son los triángulos ADC y BDC.
· El triángulo ADC:
Por lo tanto:
· Para el triángulo BDC:
Por lo tanto:
Se tiene un sistema de dos ecuaciones que se resolverán por igualación.
Sustituyendo en:
Recuerda que una razón es el cociente entre dos lados de un triángulo rectángulo. Esta relación establece las seis razones trigonométricas: seno, coseno, tangente, secante y cotangente. Aprender a utilizar estas razones, podrá, en un futuro cercano, darte la oportunidad de diseñar software, juegos, mapas geográficos, programas de dibujo y si quieres, diseñar construcciones.