Las identidades trigonométricas son igualdades que involucran funciones trigonométricas. Estas identidades son siempre útiles para cuando necesitamos simplificar expresiones que tienen incluidas funciones trigonométricas, cualesquiera que sean los valores que se asignen a los ángulos para los cuales están definidas estas razones. Las identidades trigonométricas nos permiten plantear una misma expresión de diferentes formas. Para simplificar expresiones algebraicas, usamos la factorización, denominadores comunes, etc. Pero para simplificar expresiones trigonométricas, utilizaremos estas técnicas en conjunto con las identidades trigonométricas.
Debemos conocer algunos términos que usaremos bastante en trigonometría, que son las funciones más importantes dentro de esta. El coseno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto adyacente y la hipotenusa:
Otra función que utilizaremos en trigonometría es “seno”. Definiremos seno como la razón entre el cateto opuesto y la hipotenusa en un triángulo rectángulo:
Mientras tanto que la palabra tangente en matemática puede que tenga dos significados distintos. En geometría se utiliza el termino de recta tangente. Pero, a nosotros en trigonometría, nos interesa otro termino, el de tangente de un ángulo. En este caso nos referimos a la relación entre los catetos de un triángulo rectángulo, lo mismo que decir, que es el valor numérico que resulta de dividir la longitud del cateto opuesto entre la del cateto adyacente al ángulo.
Ejemplo.
Considerando el péndulo cónico, con una plomada de 80 kg, en un alambre de 10 metros, formando un ángulo de u=50 con la vertical, representado en la siguiente imagen:
Determina:
a) Las componentes vertical y horizontal de la fuerza ejercida por el alambre en el péndulo:
b) La aceleración radial de la plomada.
Tambien las identidades trigonométricas son igualdades comprobadas que muestran la relación entre ángulos. En la física son importantes, ya que por medio de la igualdad se pueden obtener los datos para resolver un problema.
|
Identidades reciprocas |
||
|
Identidades por cociente |
||
|
Identidades Pitágoras |
Las identidades trigonométricas permiten plantear una misma expresión matemática de diferentes formas. Es importante señalar que las identidades son útiles cuando se necesitan simplificar expresiones que tienen incluidas funciones trigonométricas, cualquiera que sea el valor que se asigne a los ángulos para los cuales están definidas estas razones.
¿Cómo se puede representar una función trigonométrica con base en las otras?
A partir de la igualdad trigonométrica se sustituyen las identidades, luego se simplifican para comprobar que se sigue manteniendo la proporción. En los siguientes ejemplos se muestra los pasos para comprobar la igualdad entre las diversas identidades trigonométricas.
Ejemplo 1.
Comprobar la siguiente igualdad trigonométrica:
Paso 1.
Las expresiones involucradas en la fracción tales como cotangente (cotx), secante(secx) y cosecante(cscx), se sustituyen en términos de senos y cosenos.
Paso 2
Se simplifican las igualdades y queda comprobada la igualdad.
Ejemplo 2.
Comprobar la siguiente igualdad trigonométrica cos2x – sen2x = 2 cos2x −1. Se utilizará el lado izquierdo de la igualdad, aplicando la igualdad pitagórica la cual dice que el sen2x + cos2x = 1, de aquí se despeja sen2x = 1 − cos2x y se sustituye en la expresión anterior.
El signo – (menos) afecta a todo lo que está dentro del paréntesis:
Como habrás observado en los ejemplos anteriores, las identidades trigonométricas son útiles para simplificar relaciones y resolver de forma más fácil los modelos matemáticos.

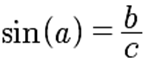



![clip_image002[3] clip_image002[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgOFp1odnh_IHFcjqGNdslBIiP4CmmAw4QKxGygGjFYwdqSs7c5Qp1diLtEkwU2EviJqlkY9TOUd9ri3Uqv_pXVGXyBYo27k6LVkIuFipDM6G4bTiJlon3M5SBLTBPYhidnd0kM8UJK4lRX/?imgmax=800)
![clip_image004[3] clip_image004[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjPtEDX7eXFyfyFTV9GR0xu5D3KJeSLJDBHTcMPAE_V9ukfsIOIgdB0MuRhY0RL2oAUCrllMtb54EnEw4o1txbp1d3Gc78tIg7lT0UQ_i2WVH4PZ-6hRq0-TOPIOR_i2NSGzRFS-N82yDa-/?imgmax=800)
![clip_image006[4] clip_image006[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgVpE9zp-2JGKoXRBPnbWT4IRGtJBgEuJgDSr3GnsS2MX9wA9YU5iyjHH6OlII2en5nUyvAFwFbcYL35AqJ-aIAZfzmhFtFw96YRg8yzgZusHzxXP51Y2TwS-wL-nAaM3TZhRRwUOeXwqVb/?imgmax=800)
![clip_image008[4] clip_image008[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjHATlaohznJWAyj0pdI-AIDfZJndxbz2j8hdtxdEGmyDu2ZSmUdkuwTZ6MBwSpefxxnBLeoSz3U17_9-pEM23sgN3SqrK-EnjHipkIgKB38S0OuQbVVzQLm3bBDaVj6lajWi-4QfJcRT4P/?imgmax=800)
![clip_image010[4] clip_image010[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi1zqnY9JpZ-RnCkgRNtQ7g09dfo18vvx-_79AKokJfy2g2SwJYrX2JRozlI0SaTJTS49mlSDLr0nNq7nmG5OcmUzGnaj30JjEWyNa1KBU_2LwtUO10n8EqR2mT2HYp6aKfmSNrduliQMIo/?imgmax=800)
![clip_image012[3] clip_image012[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgXBJ3M3HXm71h94ghdzDzvmQ4eKfYTK7kaH8YP6rp-UiwBl0o2o0H2MviFDU36q2-bPbTZ9WLeF1Ce197awUfGhl_p23cgkyshVg2rvbHKctCmmoWGTATsJi_iz2H3XzwsPBfuX5uWz0hn/?imgmax=800)
![clip_image014[3] clip_image014[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhUms0OxvezWoPSH6GLzV0zByjwYh4qPrdNPOTmgZ4hCEI4BY6GzAO3MeJUZ4jjGfIUS31b8EH-kK8nQQISKzvF9tzspsQel6HTZLO3FWZra3dvGSrktcEt_VJbxF1HQfe0_gfUb_mGSXfm/?imgmax=800)
![clip_image018[3] clip_image018[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiCus_7UaJjOnJ2E86PN0zsw1RZkv7WrFxgd9M5ESkHj0yarKvmQFtk6r6GnyTguE125ZfhXzEnA_FKQFdYYPQXsu6H_SEKjsc5Q3fV6VIOdhA4zhRORWqDkH40PeM5vU6Se4hh7Wtes388/?imgmax=800)


