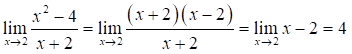Continuidad.

Conceptos.

La idea de la continuidad está implícita en el uso diario de las matemáticas elementales. Intuitivamente, una función ƒ es continua si su gráfica no contiene interrupciones, ni saltos, ni oscilaciones indefinidas. Aunque esta descripción es, por lo general, suficiente para decidir si una función es continua, es decir observando simplemente su gráfica, es fácil caer en el engaño. Imagina una función ƒ que tiene el valor ƒ(x ) en un cierto punto p. Se dice que ƒ es continua en a, si en todo punto próximo x el valor de la función ƒ(x ) es próximo a ƒ(a ). Otro modo de expresar este hecho es el siguiente: si x se mueve hacia p, el valor correspondiente de la función ƒ(x ) debe llegar a ser próximo a ƒ(a) como se desee, cualquiera que sea la forma con que x tienda a a. En los valores de una función continua no se presentan saltos bruscos, como se muestra en la siguiente figura.

Cuando empezó a desarrollarse el cálculo, la mayor parte de las funciones con las que se trabajaba eran continuas y, por lo tanto, no se sentía la necesidad de profundizar en el significado de continuidad. En el siglo XVIII se presentaron algunas funciones discontinuas en relación con distintos problemas físicos, en particular sobre la Teoría Calórica. Esto obligó a los matemáticos de principios del siglo XIX a examinar cuidadosamente el significado de los conceptos de función y continuidad. Una definición matemática satisfactoria de continuidad, expresada enteramente por medio de las propiedades del sistema de los números reales, fue la que formuló Augustin Louis Cauchy. Su definición, que aún se da hoy día, puede exponerse más fácilmente por medio del concepto de límite. Sea ƒ(x ) una función cualquiera en un intervalo abierto que contenga un punto a, y sea L un número real.

Entonces:

La fórmula dice que el límite de ƒ(x ), cuando tiende a , ƒ(x ) tiende a ƒ(x ) cuando x tiende a . Esto implica la idea de que ƒ(x ) puede hacerse tan próximo a como L se desee, con tal de que x se elija suficientemente próximo a .

Por otro lado, cualquier intervalo abierto que contenga un punto a como su punto medio se denomina entorno de a.

Se designan estos entornos con (L− 𝜀, L + 𝜀), (a − , a + ), etcétera. Puesto un entorno (a − , a + ), es un intervalo abierto simétrico respecto a , consta de todos los números reales x que satisfacen a − < x < a + .

Ahora, si L es un número real y ƒ es una función definida en un cierto entorno de un punto L, entonces:

Significa que para todo entorno (L− 𝜀, L + 𝜀) existe un cierto entorno (a − 𝛿, a + 𝛿) tal que:

ƒ(x)𝜀 (L− 𝜀, L + 𝜀) siempre que x (a − 𝛿, a + 𝛿) y x ≠ a

Lo primero que se observa en esta definición es que en ella intervienen dos entornos, (L− 𝜀, L + 𝜀) y (a − 𝛿, a + 𝛿). El entorno (L− 𝜀, L + 𝜀) indica cuán próximo se quiere sea ƒ(x) a su límite L. El segundo entorno (a − 𝛿, a + 𝛿), indica lo próximo que debe estar x de para que ƒ(x) sea interior al primer entorno (L− 𝜀, L + 𝜀). Lo esencial de la definición es que para cada (L− 𝜀, L + 𝜀), por pequeño sea, existe un cierto entorno (a − 𝛿, a + 𝛿) que satisface las condiciones anteriores. En general, el entorno (a − 𝛿, a + 𝛿) dependerá del (L− 𝜀, L +𝜀 ) elegido. Un entorno (a − 𝛿, a + 𝛿) que sirva para un (L− 𝜀, L + 𝜀) determinado servirá también, para cualquier (L− 𝜀, L + 𝜀) mayor, pero puede no ser útil para todo (L− 𝜀, L + 𝜀) más pequeño.

El límite puede representarse geométricamente en la siguiente figura. En el eje está representado el entorno (L− 𝜀, L + 𝜀). El entorno correspondiente a (a − 𝛿, a + 𝛿) se ha representado en el eje .

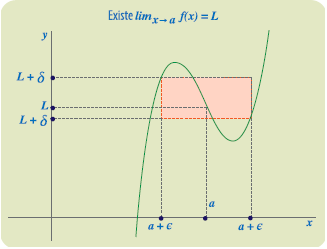
El rectángulo consta de todos los puntos (x, y) para los cuales x (a − 𝛿, a + 𝛿) y y (L− 𝜀, L + 𝜀). La definición de límite asegura que toda la gráfica de ƒ correspondiente está situada en un rectángulo, salvo para el mismo punto a.

Es costumbre designar el radio de (L−𝜀,L +𝜀 ) por   y el de (a − 𝛿, a + 𝛿) por . Decir que ƒ(x)𝜀(L−𝜀,L+𝜀) es equivalente a la desigualdad |ƒ(x)−L|< 𝜀, y poner que x𝜀(a − 𝛿, a + 𝛿), x ≠ a es lo mismo que escribir 0 <|x−a|<𝛿. Por lo tanto, la definición de límite puede expresarse de la siguiente forma:

Significa que para todo 𝜀> 0, existe un 𝛿> 0 tal que:

| ƒ(x) − L | < siempre que 0 < | x − a | <𝛿

En la definición de límite no se hace mención del comportamiento de ƒ en el punto a. Como ƒ(x)(L−𝜀, L+𝜀) siempre que x (a − 𝛿, a + 𝛿) y x ≠ a. Se refiere a aquellos puntos x ≠ a pertenecientes al entorno (a − 𝛿, a + 𝛿), con lo que no es necesario que esté definida en a. Además, incluso si ƒ está definida en c, su valor allí no es necesariamente igual al límite L. No obstante, si ocurre que ƒ está definida en a y que ƒ(a)=L, se dice entonces que la función ƒ es continua en a.

Condiciones

En la definición de límite se hizo énfasis en la restricción x ≠ a, como se vio en la sección anterior en algunos ejemplos de límites. Ahora se presentan varias funciones que no son continuas en un punto a y se clasifican dichas discontinuidades.

En las gráficas se muestran varias funciones que no son continuas en a y se indican los nombres de dichas discontinuidades. En el caso de (i) los límites por la derecha y por la izquierda existen, pero son distintos y, por lo tanto, el límite no existe en a. Para la discontinuidad infanta no existe el límite, ya que los límites laterales no existen. Para el caso (iii) y (iv) son parecidas porque el límite existe en ambos casos, además en los dos en (iii) no está definido y en (iv)

Una función es continua en si se satisfacen las tres condiciones siguientes:
	ƒ está definida en un intervalo abierto que contiene
	existe

A veces es conveniente pensar en las funciones que son continuas, imaginarlas en un intervalo, como el caso cuya grafica se puede trazar sin levantar el lápiz del papel. Una interpretación mas formas es que una modificación el el valor de x produce un cambio pequeño en el valor de f(x). Esto se debe a la definición del limite.

Si Si f es una función definida como:

Donde su grafica es:

Se observa que es una recta. Sin embargo, la definición indica que tiene una discontinuidad en el punto x-2, entonces el limite de la función se calcula de la siguiente manera:

Por lo tanto, la función tiene una discontinuidad removible en ese punto, por lo que la función se puede definir de la siguiente forma:

La función tiene su dominio en el conjunto de los números reales R, el cual es abierto. El limite. donde esta la discontinuidad, existe y es –4. Por ultimo, se tiene que f(-2)-(-4), el cual coincide con el limite, por lo que se cumplen las condiciones de la definición, siendo la función continua, todos los puntos del abierto, en este caso es R

Si las funciones f y g son continuas en a, esto es:

Entonces se cumple:

Estos resultados se pueden generalizar en mas de dos funciones, es decir, a tres o mas funciones continuas, siempre y cuando no se anulen en el denominador.

Si g es continua en a y f es continua en b y g(a)-b, entonces:

Sea f(x)=e^x y g(x)=x², entonces la composición define una nueva función h(x) = ((g)x) =e^x2, entonces la función h(x) es continua en todo punto:

La función es continua en todos los puntos, ya que las funciones ƒ(x) = e^x y g(x) = x² son continuas en todo punto.

La continuidad es uno de los temas mas importantes del calculo, ya que formalizan el concepto de aproximación hacia un punto de una fracción, la cual es un pilar fundamental del calculo infinitesimal.