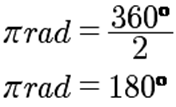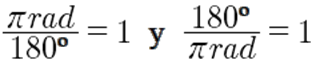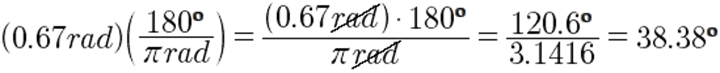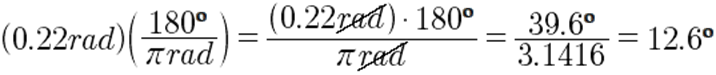Definición de ángulos.
Ángulo hace referencia a una figura de la geometría que se forma a partir de dos rectas que se cortan entre sí en una superficie.
Posición angular.
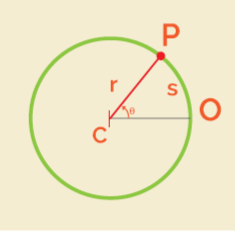
La posición angular, en un instante de tiempo, del objeto en movimiento se encuentra en el punto P. la posición angular q viene dada desde el punto P, en el centro de la circunferencia C y el origen de los ángulos O.
De donde q = posición angular es el cociente (división) entre la longitud del arco s y el radio de la circunferencia r.
La posición angular es el cociente (división) entre dos longitudes y, por tanto, no tiene dimensiones.
Medidas angulares.
Radian (rad) es la medida del ángulo central de una circunferencia cuya longitud de arco coincide con la longitud de su radio.
Ejemplo.
En varias ocasiones habrás escuchado:
· El barco cambio de rumbo 30º al Norte.
· La ventana tiene un ángulo de 90º
· Un motor gira a 50 radianes por segundo.
· La pelota de beisbol fue lanzada a una curca de 2 rad por segundo.
Aunque las dos unidades equivalentes de desplazamiento angular, el radian se utiliza porque facilita la realización de diversos ángulos. Debido a la utilidad de ambas unidades a continuación te explicaremos como se realizan las conversiones entre ellas.
La fórmula es:
Despejando para simplificar:
Si rad =180º entonces:
Para convertir una unidad y no se poder la igualdad, el número se multiplica por 1, y se utilizan las igualdades de arriba para esto.
Hay que fijarnos que la unidad que se utilice contenga las unidades, de tal forma que se eliminen una con otras en la división.
Para recordar que el valor de es 3.1416
a) Conversión de radianes a grados.
· Convertir 0.67 radianes a grados:
· Convertir 0.22 radianes a grados:
b) Convertir de grados a radianes.
· Convertir 30º a radianes.