Ecuaciones lineales en movimientos circulares

Concepto de ecuaciones lineales en movimientos circulares.

Recordemos que una ecuación lineal es la que solamente involucrara sumas y restas de una variable a la primera potencia. Usaremos estas ecuaciones lineales para cada una de las expresiones algebraicas, o sea los valores conocidos, y por otra parte las incógnitas que son justamente aquellos valores por descubrir. Por medio de diferentes operaciones matemáticas podremos conocer los datos desconocidos que nos ayudaran a entender los fenómenos físicos derivados del movimiento circular.

Velocidad angular y velocidad tangencial.

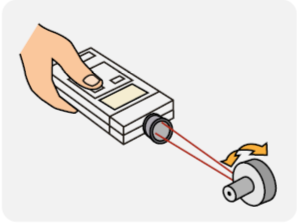
Los motores son maquinas giratorias que se utilizan en muchos lugares, en cuyo caso uno de los parámetros que es importante controlar es la velocidad con la que giran, ya que cada aplicación necesita una velocidad especifica de acuerdo con su función.

El tacómetro es un instrumento para medir la velocidad de rotación de un mecanismo de la maquina al que va acoplado; generalmente, indica la velocidad en revoluciones por minuto.

La velocidad angular es una medida de la velocidad de rotación. Se define como el ángulo girado por una unidad de tiempo y se designa mediante la letra griega y. Su unidad en el Sistema Internacional es el radian por segundo (rad/s).

La velocidad tangencial V es igual a la velocidad angular por el radio. Se llama tangencial porque es tangente a la trayectoria.

Siendo:

         r = radio

         v = velocidad

Como habrás notado, en el primer párrafo se menciona que las unidades de velocidad de rotación están en revoluciones por minutos (rev/min) y en el segundo en radianes por segundo (rad/seg), las dos son unidades de velocidad angular y aquí te mostramos la equivalencia.

Equivalencia: Una revolución = 2 radian = 360º

Aunque las dos unidades son equivalentes del desplazamiento angular, el radian se utiliza porque facilita la realización de diversos cálculos debido a la utilidad de ambas unidades.

Para comprender mejor las unidades de la velocidad angular te mostrare dos ejemplos.

Una rueda de la fortuna gira aproximadamente:

Un motor de licuadora gira a:

Ejemplo.

Cuando se realiza una carrera ciclista gana el que logra una mayor velocidad angular durante más tiempo ya que esa velocidad angular se convierte en velocidad tangencial, la cual hace desplazarse a los competidores. Esta relación permite establecer ecuaciones lineales para entender el comportamiento de estas variables y constantes. De tal manera, que, si todos los competidores usan llantas del mismo tamaño, con la magnitud de radio podemos calcular la velocidad de desplazamiento de la bicicleta. Esta relación que existe entre estas fuerzas la podemos expresar con una función lineal donde:

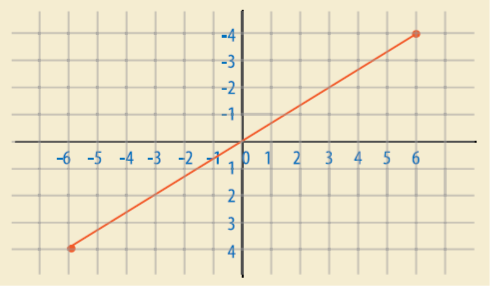
de tal manera que si graficáramos la función nos queda:

Grafica de la ecuación como una recta que pasa por el origen y con una pendiente de 45º