Definición
¿Has observado el tipo de movimiento que experimentan
los balones al ser golpeados en diversos deportes que se practican de forma
cotidiana?
El movimiento que describe un balón al momento de ser
pateado o golpeado es un parabólico porque se mueve con una trayectoria curva.
En este movimiento la aceleración debido a la gravedad es constante en todo el
recorrido y esta dirigida hacia abajo.
El movimiento es una combinación de los movimientos
rectilíneos, uniformemente acelerado y caída
libre.
Componentes del tiro parabólico
Para ilustrar los componentes de un tiro parabólico
imagina el lanzamiento de un proyectil.
Para que se origine el tiro parabólico, el proyectil
debe ser lanzado con un ángulo mayor a 0º y menor a 90º (si fuera 90º seria un
tiro vertical y no parabólico). Este ángulo se representa con la octava letra
del alfabeto griego, la cual se denomina theta ø.
Ademas el proyectil debe lanzarse con una velocidad
inicial representada por V0.
Identifica en la figura anterior los dos elementos
nombrados:
· Ángulo ø
· Velocidad inicial v0
La velocidad inicial con la que se lanza el proyectil
tiene dos componentes V0x
y V0y,
los cuales se calculan con las siguientes
fórmulas.
Identifica en la figura anterior los dos elementos
nombrados:
· El componente en el eje de la velocidad inicial
(V0x)
· El componente en el eje de la velocidad inicial
(V0y)
Para cualquier instante del movimiento, la velocidad
del proyectil tiene dos componentes (Vx y Vy). la
posición también tiene las dos coordenadas (x,
y)
Verticalmente el movimiento
es uniformemente acelerado. La única fuerza que actúa sobre el proyectil es la
gravedad, por lo que la aceleración
es g.
Para cualquier instante del movimiento, la velocidad
vertical (Vy) debe calcularse como si fuera un lanzamiento
vertical. Observa en la figura que en el punto más alto de la
trayectoria el componente de la velocidad en el eje
es igual a cero (vy = 0).
Esto sucede porque en este punto ya no existe ninguna fuerza que impulse al
proyectil de forma vertical, debido a que alcanzó su máxima altura.
Horizontalmente la velocidad es constante
Vy=VoVy
coseno Ø y debe calcularse como si fuera un movimiento
rectilíneo uniforme.
Para todos los proyectiles lanzados con el mismo
impulso, la altura máxima, el alcance horizontal y el tiempo están determinados
por el ángulo de salida.
Calculo del tiro parabólico.
Ejemplo.
Se patea un balón de futbol con un ángulo de 30º, con
una velocidad de 20m/s. calcula:
a) La altura
máxima
b) El tiempo que
permanece en el aire
c) La
distancia a la que llega al suelo
d) La
velocidad en cómo cae el balón después de 1s de haber sido
pateado.
Datos:
Paso 1.
Calcula los componentes de la velocidad
inicial.
Recuerda que:
Sustituyendo:
Paso 2.
Paso
3.
Calcula la altura
máxima.
Paso 4.
Calcula
El tiempo
total. En este caso solo se multiplica el tiempo de altura máxima por 2 porque
se sabe que la trayectoria, es simétrica y el proyectil tarda el doble de tiempo
en caer que de lo que tarda en alcanzar la altura
máxima.
Paso 5.
Calcula el alcance máximo. Recuerda que la
distancia es igual a la velocidad por el tiempo (d=v·t),
por lo tanto, si se quiere calcular a que distancia del inicio caerá el balón,
se usa la siguiente fórmula:
El balón caerá a 38.96m del
origen.
Paso 6.
Calcular la velocidad de X como en el balón después de
un segundo de haber sido pateado. Para calcular la velocidad en X, se emplea la
siguiente fórmula:
La velocidad en
es la misma del componente en x de
la velocidad inicial calculada en el paso 1vox=vfy=15.97m/s
porque es constante durante todo
el movimiento.
USO DEL SIMULADOR DE TIRO PARABÓLICO
En este subtema se
utilizará un simulador para obtener las respuestas del
siguiente
problema:
Un proyectil es
disparado a una velocidad de 15 m/s con un ángulo de
45°.
a)
¿Cuál
será su altura máxima?
b)
¿Cuál
es el alcance máximo?
c)
¿Cuál
es el tiempo que permanece en el
aire?
Paso
1
Accesar a la página http://www.educaplus.org/movi/4_3tparabolico.html y ubica
la
sección donde se
encuentra el simulador.
Paso
2
Se ingresan el
valor de la velocidad en m/s y el valor del
ángulo.
Paso
3
a) ¿Cuál será su altura máxima?
b) ¿Cuál es el alcance máximo?
c) ¿Cuál es el tiempo en el que permanece en el
aire?








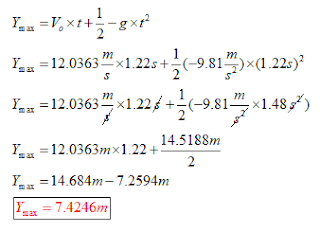
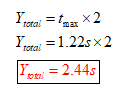








No hay comentarios.:
Publicar un comentario