El calculo infinitesimal fue un paso importante en el desarrollo de las matemáticas. Este paso se dio en el siglo XVII con los trabajos de Newton, en Inglaterra, y Leibniz, en Alemania. Con este recurso metodológico, desde entonces, se han podido resolver problemas que parecían imposibles de comprender, tales como el contenido del vino en un barril, o el tiempo de desplazamiento de un objeto, entre otros muchos. En la actualidad, el calculo infinitesimal permite conocer el movimiento de los huracanes y predecir su posible incidencia en el ambiente, o la trayectoria que debe seguir una nave espacial para llegar a la Luna, o la cantidad de agua que se debe desplazar y el tamaño de las tuberías para abastecer de agua a una comunidad, entre muchos otros aspectos necesarios para la sociedad y el sostenimiento del medio ambiente.
El calculo, sin embargo, tiene en los limites sus pilares más importantes porque contribuyen a resolver eficazmente los problemas que se presentan en ejercicios de termas específicos. Cada límite puede dar una solución diferente. Por ejemplo, la solución a un ejercicio podría conseguirse con una función indeterminada, la cual resulta cuando es igual a cero sobre 0/0. Así también se pueden encontrar funciones con soluciones o funciones determinadas. Por esta razón, el primer paso es adentrarse al tema del calculo que es el estudio de la concepto límite en las matemáticas.
Límites laterales.
En algunas funciones, como las definidas por partes o discontinuas, se aplican los límites laterales. En las funciones con radicales de índice par, no se puede hablar del límite en los extremos del dominio de la función. El estudio de las funciones definidas por partes o discontinuas sirve para establecer si tienen límites en los puntos donde la función cambia de forma y, en caso de que lo tenga determinar su valor.
Es importante recordar el concepto de intervalo abierto denotado como:
Donde y no pertenecen al intervalo abierto:
Se supone que una función f está definida en un intervalo (a,b). Se dice que el límite de f, cuando x tiende a c por la izquierda, es L si f(x) se acerca a L cuando x se acerca a c para valores donde x<c. Esto se escribe como:
Estas son solo las nociones formales de límites laterales. La definición formal contempla ambas situaciones. Entonces:
Sea la función: R → R definida de la siguiente manera:
Se observa que la función está definida en todo R; lo que significa que está bien. Ahora, se toma al punto c=0, y se aplica el límite por la izquierda, de tal manera que se tomarán valores x≤0. Como en este tramo la función es constante –1, el límite al que tiende la función es –1, es decir:
De la misma manera, se tiene algo similar para el límite por la derecha: si c<x, implica que 0<x, lo que quiere decir que los valores de siempre son positivos. Como la función por ser la constante 1 de lado de los valores positivos, se tiene que el límite se puede ver como:
En este caso, el límite no existe, ya que son distinto, con lo que se puede concluir que si los límites laterales existen y son iguales, el límite en un punto existe, es decir:
Ahora, sea la función:
Evaluar:
En la gráfica aparece un croquis de función f.
Por lo que los límites por la izquierda y por la derecha existen y son iguales, por lo tanto:
Sea la función f(x)=x2, si x tiende a 2, el límite es L=4. Construyendo las siguientes tablas de valores próximo a 2, anteriores y posteriores:
Cuando x se aproxima a 2, por la derecha y por la izquierda, los valores de |f(x)|, tan pequeño como se quiera, haciendo |x-a| suficientemente pequeño, pero x≠a.
Si la función f tiende hacia el límite L en a, significa: para todo periodo 𝜀>0 existe de algún >0 o tal que, para todo x, si 0<|x-a|<𝛿, entonces |f(x)-L|<𝜀. Esta definición es muy importante, ya que todo lo que se aprenda, a partir de ahora, depende de ella, por lo que sería inútil detenerse a causa de ella. Memorizala si es necesario.
Recuerda las propiedades de valor absoluto, en particular la propiedad donde 0<|a|<b.
Si la función f tiende hacia el límite L en significa: para todo 𝜀>0 existen algún 𝛿>0 tal que, para todo x, si 0 < − a <𝛿, entonces ƒ(x) − L<𝜀 o L− ƒ(x) <𝜀.
Es decir:
Si los valores de x <a, la función ƒ tiende hacia el límite L en , significa: para todo 𝜀>0 existe algún 𝛿>0 tal que, para todo x, si 0 <a− <𝛿, entonces ƒ(x) − L <𝜀 ó -
ƒ(x) <𝜀.
Es decir:
Como puedes observar, de la definición de límite surgen las definiciones de límites laterales, por lo que se puede concluir que si existen.
|
Sea la función
|
|
dada como
|
|
, donde se puede
observar
|
|
que el dominio de la función es el intervalo
(0,1).
| ||||
Ahora, se va a valvular el límite cuando tiende a-1 por la derecha, es decir –1<. Para valores fuera del dominio no tiene sentido la función, por lo que solo se puede encontrar el límite por la derecha:
Y por la izquierda cuando tiende a 1, es cuando <1, por lo que queda:
Los límites laterales existen para 1 y –1 y ambos son cero. Sin embargo, los límites por la derecha y por la izquierda, respectivamente, no existen. Dado que la función no está definida en los intervalos (∞,−1) y en (1,∞).
Una función no puede tender hacia dos límites en . En otros términos, si ƒ tiende
hacia L en , y hacia en , entonces l = m. Es decir, sólo existe un único límite.
hacia L en , y hacia en , entonces l = m. Es decir, sólo existe un único límite.
Sea:
Determinar el limite cuando x=3
Este límite, como se observa, es indeterminado, ya que (3-3)(3+4)(3-7)=0, el denominador es cero, por lo tanto se le nombra, limite indeterminado. Sin embargo, se puede usar álgebra y factorización para simplificar la expresión a otra similar. En el próximo ejemplo se dará la respuesta del límite indefinido, realiza las operación necesarias para dar solución al limite. La finalidad es recordar las operaciones algebraicas, practicarlas.
Límites al infinito.
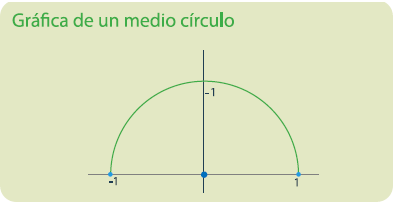
Se desea calcular el valor de 𝜋 con el mínimo error. Se sabe que el área del circulo de radio 1 es igual a 𝜋. De manera intuitiva es posible encontrar la forma de ir aproximándose:
Si se sabe que el área del circulo de radio 1 es 𝜋, entonces al ir dibujando polígonos regulares dentro del circulo y calcular el área de cada uno se puede aproximar al área del circulo. Cuando n se aproxima al infinito, se obtiene el valor aproximado de 𝜋.
Es decir, el límite del área del polígono inscrito en la circunferencia unitaria, cuando su numero de lados tiende a infinito, es 𝜋.
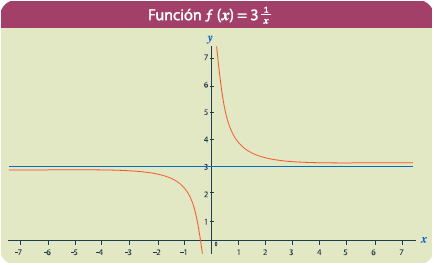
Considera primero la función:
|
-1+
|
100
|
1000
|
10000
|
100000
|
|
F(x)
|
3.01
|
3.001
|
3.0001
|
3.00001
|
Entonces, el limite se expresa como:
|
Lo
cual se lee de la siguiente forma: el límite
de:
|
cuando
x tiende a infinito, es
3.
|
Es importante recordar que no se puede sustituir nunca la variable x por ∞, puesto que no es un numero real. Entonces, la expresión x tiende ∞ significa que se le asignan valores muy grandes a x.
En general:
Significa que para toda 𝜀>0, existe un número positivo N tal que | f(x)-L|<𝜀, siempre que, x>N. Sea:
Considerando dos rectas horizontales:
De acuerdo con la figura, cualquier x mayor que una cierta N, cualquier punto (xf(x)) se encuentra entre estas dos rectas. La recta y=N es una asíntota horizontal de la gráfica de f.
En la figura, la gráfica se acerca desde abajo a la recta L, es decir f(x)<L. La siguiente definición abarca este acaso. Si:
Significa que para toda 𝜀>0, existe un número negativo N tal que |ƒ (x ) − L | <𝜀 siempre que x<N. Sea:
Si se consideran dos rectas horizontales y = L ± 𝜀. Entonces, cuando x es menor que
cierto número negativo N, todos los puntos (x,ƒ(x )) de la gráfica se encuentran
entre ellas. Dada la función:

Encontrar las rectas asintóticas, es decir donde la función esta indefinida o tiene una
recta asintótica horizontal.
Primero, se encuentran las rectas asintóticas horizontales para luego calcular el límite cuando x tiende a ∞.
Primero, se encuentran las rectas asintóticas horizontales para luego calcular el límite cuando x tiende a ∞.

y los límites:
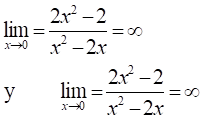

En la figura se muestran las asíntotas de color rojo correspondientes a los límites, donde el límite se indefine y se hace infinito.
![clip_image002[6] clip_image002[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEizgxCTopnCscH84K6hxWEb78mfOi8raWBxMCUIN2ChARV6agDIPjkM3BawmC1Bh9xchHhmYzceuRcdLt1TzkxGAq17o2jnN9aKubjDGQGX-X9jy49AIeh1fcxNzfC_dCKnRQn4UJr8DRfk/?imgmax=800)


![clip_image002[18] clip_image002[18]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgM6FHqQa9YFOjOP7fx0XSs1a_vD2fxANoqMclN61ICxScoNTZ5NZTAgqufTk4WkmQF_26a70BANLJN5-g1oQSNbNmhyphenhyphen4sfL65SIfRXJgn49r8hqLnYN0WbdWpCNlOTZ7JangZyvhhS-odb/?imgmax=800)










No hay comentarios.:
Publicar un comentario