Para poder
encontrar la mediana de una colección de datos es necesario primero ordenarlos
de manera creciente.
En una hoja de calculo puede usarse la función =MEDIANA( ), seleccionando los datos a los cuales se les quiere obtener la mediana.
Moda.
Es simplemente el datos que mas se repite en otras palabras, es el de mayor frecuencia. Puede determinarse en una hoja de calculo mediante la función =MODA( ). Si más de un dato se repite con la misma frecuencia, todos son la moda; pero si todos son distintos, no hay moda. También para este caso los datos no necesitan ser números pues solo hasta con que tenga la mayor frecuencia.
Rango medio.
Es el promedio de los valores máximos y mínimos de todos los datos.
Considera el siguiente caso para mostrar la obtención de las medidas de tendencia central a partir de una tabla de distribución de frecuencias.Encuentra la media, la mediana, la moda y el rango medio de la siguiente colección de datos.
Valor
|
Frecuencia
|
25
|
18
|
31
|
8
|
42
|
6
|
59
|
4
|
94
|
3
|
Para la media es necesario agregar la columna Valor por frecuencia y la fila de las sumas.
Valor
|
Frecuencia
|
Valor x
Frecuencia
|
25
|
18
|
450
|
31
|
8
|
248
|
42
|
6
|
252
|
59
|
4
|
236
|
94
|
3
|
282
|
Suma
|
39
|
1468
|
Entonces el promedio esta dado por:
Para obtener la mediana.
Ya que se tienen 39 datos, el que se encuentra en el medio debe ser el dato 20, ya que tiene 19 datos menores o iguales que él y 19 mayores o iguales que el. De acuerdo con la tabla los primeros 18 datos son 25, así que el que se encuentra en el lugar 20 es 31.
Entonces la mediana es igual a 31.
La moda es fácil de determinar, viendo la tabla donde el dato con mayor frecuencia es 25.
Y por último, el rango medio es el promedio entre el dato menor 25 y el mayor 94:
Estimación de medidas de tendencia central a partir de la tabla de frecuencias agrupadas.
Hasta el momento se han calculado las medidas, en caso de que los datos no sean agrupados. Sin embargo tambien es posible aproximar estos valores a partir de la tabla de frecuencias agrupadas. Esto es útil cuando son muchos datos muy diferentes, como en la siguiente tabla con datos generados aleatoriamente con ayuda de Excel y la formula =ALEATORI.ENTRE(0.50).
0
|
6
|
4
|
42
|
37
|
10
|
46
|
1
|
39
|
14
|
24
|
0
|
15
|
15
|
12
|
23
|
48
|
18
|
9
|
26
|
17
|
42
|
31
|
0
|
25
|
14
|
41
|
0
|
4
|
40
|
46
|
39
|
1
|
6
|
0
|
8
|
34
|
23
|
23
|
31
|
14
|
43
|
29
|
28
|
1
|
24
|
36
|
42
|
22
|
32
|
11
|
25
|
50
|
15
|
3
|
34
|
46
|
18
|
6
|
16
|
24
|
40
|
35
|
38
|
48
|
4
|
39
|
31
|
0
|
41
|
40
|
14
|
26
|
29
|
3
|
16
|
14
|
48
|
1
|
36
|
Primero, se elabora la tabla de datos agrupados. Los valores usados se calculan también con ayuda de Excel, de tal manera que los valores necesarios quedan como se muestra en (1).
La tabla de frecuencias de datos agrupados queda de la siguiente forma como se muestra en (2).
(1)
N
|
Máximo
|
Mínimo
|
Rango
|
Número de clases
|
Amplitud de clase
|
80
|
50
|
0
|
50
|
7
|
7
|
(2)
Clase
|
Limites de
clase
|
Marca de
clase
|
Frecuencia
|
No.
|
Li
|
Ls
|
mi
|
fi
|
1
|
0
|
7
|
3.5
|
18
|
2
|
8
|
15
|
11.5
|
12
|
3
|
16
|
23
|
19.5
|
10
|
4
|
24
|
31
|
27.5
|
13
|
5
|
32
|
39
|
35.5
|
11
|
6
|
40
|
47
|
43.5
|
12
|
7
|
48
|
55
|
51.5
|
4
|
Para determinar la media se puede considerar la marca de clase y la frecuencia de clase. Con este paso, se asume que la marca de clase sustituye las apariciones de toso los elementos de la clase. De esta manera se construye la tabla con los productos de la marca de clase multiplicada por la frecuencia absoluta de la clase:
Clase
|
Límites de
clase
|
Marca de
clase
|
Frecuencia
|
Marca x
frecuencia
|
No.
|
Li
|
Ls
|
mi
|
fi
|
mi
x fi
|
1
|
0
|
7
|
3.5
|
18
|
63
|
2
|
8
|
15
|
11.5
|
12
|
138
|
3
|
16
|
23
|
19.5
|
10
|
195
|
4
|
24
|
31
|
27.5
|
13
|
357.5
|
5
|
32
|
39
|
35.5
|
11
|
390.5
|
6
|
40
|
47
|
43.5
|
12
|
522
|
7
|
48
|
55
|
51.5
|
4
|
206
|
La aproximación de la media puede obtenerse como:
Este valor se aproxima al promedio de todos los datos que se tienen, y la media exacta es 22.9875, la cual está bastante cerca del resultado de la media. También es necesario considerar que a mas datos es posible que el resultado mejore aun mas.
Para obtener la mediana se agrega la columna con frecuencia acumulada y se hace la operación del número de datos entre dos. En este caso, como son 80 datos, la mediana debe estar entre las posiciones 40 y 41, por lo que debe buscarse esas posiciones y promediar las marcas de clase correspondientes:
Clase
|
Límites de
clase
|
Marca de
clase
|
Frecuencia
|
Marca x
frecuencia
|
Frecuencia
acumulada
|
No.
|
Li
|
Ls
|
mi
|
fi
|
mi
x fi
|
fai
|
1
|
0
|
7
|
3.5
|
18
|
63
|
18
|
2
|
8
|
15
|
11.5
|
12
|
138
|
30
|
3
|
16
|
23
|
19.5
|
10
|
195
|
40
|
4
|
24
|
31
|
27.5
|
13
|
357.5
|
53
|
5
|
32
|
39
|
35.5
|
11
|
390.5
|
64
|
6
|
40
|
47
|
43.5
|
12
|
522
|
76
|
7
|
48
|
55
|
51.5
|
4
|
206
|
80
|
La posición 40 está en la clase 3 y la 41 en la 4, por lo que se promedian las clases.
Entonces,
la mediana es
|
![clip_image002[52] clip_image002[52]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhtCY65SLFh1ZdMuZnR2MAaCxpjSLSzDfp99K6yboxtReRfW91ln1p97C4t9XNKWQPMOyecTnMNmf6XEjKF-DCf4IOQhjiaF5BaFL0-Qpd4U6lsJ8AeORP1dn-zRUEZo6vwYXYTHyxEEH6b/?imgmax=800) . .
|
Con ayuda de Excel también es posible
hallar la
|
media exacta, la cual para este caso coincide con la estimación que se hizo.
De la misma manera, la moda se obtiene con la marca de clase de la que tiene la mayor frecuencia, es decir 3.5. Para los datos completos, la moda es: 0. Para el rango medio se
toman en
cuenta las marcas de clase máxima y mínima:
|
|
.
|
El resultado es más grande que el rango mínimo exacto porque la última clase sobrepasa al dato mayor. Las aproximaciones que se obtienen a partir de las tablas de datos agrupados son de mucha utilidad cuando se tiene una gran cantidad de datos.
Las medidas de tendencia central dan información de los valores que pueden pensarse puntos medios en diferentes sentidos, por tanto es importante saber si estos coinciden, o su cercanía o variación. A este análisis se le conoce como sesgo y relaciona la media, la mediana y la moda.
Sesgo.
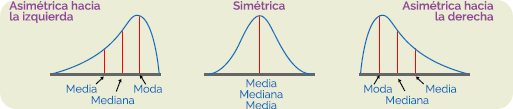
El sesgo describe la distribución de los datos, al indicar hacia donde tienden a concentrarse. La construcción de la gráfica facilita esta apreciación al mostrar los resultados de manera visual. De esta manera, una distribución puede ver:
Simétrica. Si la mayor concentración de datos se localiza en el centro de la distribución.
Sesgada a la derecha. Si la mayor concentración de datos está a la izquierda de la distribución.
Sesgada a la izquierda. Si la mayoría de los datos están concentrados a la derecha.
El comportamiento de las medidas de tendencia central, es a grandes rasgos como se muestra en la figura:
Medidas de dispersión.
Las medidas de dispersión son las herramientas que sirven para analizar la variación que presentan los datos. La primera de estas medidas es el rango. Al recordar, es la diferencia entre el dato mayor y el dato menor. Sin embargo, este resultado puede no representar el comportamiento real si existe uno o varios datos que varían mucho del resto. Estos son llamados datos aberrantes o atípicos.
La desviación estándar suele ser la más utilizada de las medidas de dispersión. Esta medida de dispersión permite observar que tan centrados están los datos, con ello se puede saber si la media es una buena representación de los datos. Si la desviación estándar es pequeña, la mayoría de los datos están cerca del promedio; si es grande, entonces están mas repartidos o dispersos. esto queda establecido en el Teorema de Chebyshev, el cual explica la desviación de las observaciones respecto a la media.
Varianza.
Esta medida es un promedio del cuadrado de las distancias de todos los datos a la media, es decir, si se tienen los datos x1 , x2 , … xn , la varianza es:
Desviación estándar.
Se define como la raíz cuadrada de la varianza:
![clip_image002[3] clip_image002[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjzwcE75T_Akwc5yG2M4SWoHdoQO1EcmWNBOZfruUbriqRkLo-vNRwvJuMsmGl3fMS7uzIdl7ivj-R8qEEuS2MzsZnbPNKTgq8VEQBTxqp2L1EKkdnyq0nC8AYrLTCOmU1xknpAs7G9Y7Kx/?imgmax=800) En una hoja de Excel es posible calcular la varianza y la desviación estándar haciendo uso de las funciones =VAR.P( ) y =DESVEST.P( ) respectivamente.
Veamos un ejemplo:
De acuerdo con los datos del INEGI en 2015, la esperanza de vida al nacer en años de edad de cada estado de la República Mexicana es:
Entidad
federativa
|
Edad
|
Entidad
federativa
|
Edad
|
Entidad
federativa
|
Edad
|
Aguascalientes
|
75.9
|
Guerrero
|
72.9
|
Quintana Roo
|
75.6
|
Baja California
|
74
|
Hidalgo
|
74.4
|
San Luis Potosí
|
74.7
|
Baja California Sur
|
76
|
Jalisco
|
75.5
|
Sinaloa
|
75.5
|
Campeche
|
75.2
|
México
|
75.2
|
Sonora
|
75.3
|
Coahuila
|
75.7
|
Michoacán
|
74.7
|
Tabasco
|
74.8
|
Colima
|
75.9
|
Morelos
|
75.7
|
Tamaulipas
|
75.8
|
Chiapas
|
75.8
|
Nayarit
|
75.1
|
Tlaxcala
|
75.2
|
Chihuahua
|
72.9
|
Nuevo león
|
76.4
|
Veracruz
|
74.1
|
Distrito Federal
|
76.1
|
Oaxaca
|
73
|
Yucatán
|
75.5
|
Durango
|
75.6
|
Puebla
|
74.8
|
Zacatecas
|
75.3
|
Guanajuato
|
75.5
|
Querétaro
|
75.4
|
Promedio Nacional
|
75
|
Se calculara la varianza y la desviación estándar para saber que tan lejos están los datos en general de la media.
Entidad
federativa
|
Edad
|
|
Aguascalientes
|
75.9
|
0.7821
|
Baja California
|
74
|
1.0315
|
Baja California Sur
|
76
|
0.9690
|
Campeche
|
75.2
|
0.0340
|
Coahuila
|
75.7
|
0.4684
|
Colima
|
75.9
|
0.7821
|
Chiapas
|
75.8
|
4.9090
|
Chihuahua
|
72.9
|
4.4759
|
Distrito Federal
|
76.1
|
1.1759
|
Durango
|
75.6
|
0.3415
|
Guanajuato
|
75.5
|
0.2346
|
Guerrero
|
72.9
|
4.4759
|
Hidalgo
|
74.4
|
0.3790
|
Jalisco
|
75.5
|
0.2346
|
México
|
75.2
|
0.0340
|
Michoacán
|
74.7
|
0.0996
|
Morelos
|
75.7
|
0.0071
|
Nayarit
|
75.1
|
0.0071
|
Nuevo león
|
76.4
|
1.9165
|
Oaxaca
|
73
|
4.0627
|
Puebla
|
74.8
|
0.0465
|
Querétaro
|
75.4
|
0.1477
|
Quintana Roo
|
75.6
|
0.3415
|
San Luis Potosí
|
74.7
|
0.0996
|
Sinaloa
|
75.5
|
0.2346
|
Sonora
|
75.3
|
0.0809
|
Tabasco
|
74.8
|
0.0465
|
Tamaulipas
|
75.8
|
0.6152
|
Tlaxcala
|
75.2
|
0.0340
|
Veracruz
|
74.1
|
0.8384
|
Yucatán
|
75.5
|
0.2346
|
Zacatecas
|
75.3
|
0.0809
|
|
Suma
|
29.6822
|
De esta manera, la varianza de
los datos es
|
![clip_image002[7] clip_image002[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiX2TRH7HGyxNEhXpormdVM2L6VQcZTxIydvzLc_4pUTNg6zz5dvUk5ivfYDLZGHvckNEPXjn4MQx0zbjoRx_AhaZjVwA6W2LbqNiLwMlNveTpEdvaK5jdJipF2gxBB7QGQw-OBUw-0Ssk3/?imgmax=800) , ,
|
y la desviación
|
estándar
|
 . .
|
Esto dice que los datos están cerca de la media, pero
también
|
Que hay variaciones considerables en algunos de los
estados.
|
Regresión y correlación lineal.
Seguramente has notado que las personas altas suelen pesar mas que las personas bajas, y este comportamiento suele mantenerse en general. Es posible hacer un estudio estadístico para determinar si estos datos ser relacionan en mayor o menor medida. Para esto, los datos se plasman en una gráfica de dispersión para luego buscar una correlación lineal entre las dos colecciones a partir de una recta que esté cerca de todos los datos, lo mejor posible. Este método se llama de mínimos cuadrados y para medir que tan buena es la aproximación se aplica el coeficiente de correlación de Pearson, lo cual se explicará a continuación.
Gráfica de dispersión.
Cuando se tienen dos colecciones de datos se establece una relación entre ellos. A cada valor de una de las colecciones le corresponde uno o varios valores de la otra. La representación de esos valores relacionados como coordenadas en el plano es llamada gráfica de dispersión.
Ejemplo. Se construirá la gráfica de dispersión con la siguiente información.
Se tomaron las altura de 9 hombres y de sus hijos, sus resultados son los siguientes.
Padre
(m)
|
1.70
|
1.77
|
1.68
|
1.75
|
1.80
|
1.75
|
1.69
|
1.72
|
1.73
|
Hijo
(m)
|
1.74
|
1.78
|
1.77
|
1.78
|
1.77
|
1.71
|
1.76
|
1.73
|
1.74
|
Al representar los datos en la gráfica de dispersión, uno de los valores será el eje X. Por ejemplo, se podrá poner la altura de los padres como coordenadas X y la altura del hijo como la coordenada Y. La gráfica queda de la siguiente manera:
Para generar el gráfico anterior en Excel, basta con seleccionar los datos de la tabla como se presento e insertar el gráfico de tipo dispersión.
Cuando se estudia la relación entre dos variables, una puede considerarse causa y la otra resultado o efecto de la primera. El supuesto de la existencia de una relación de causalidad es sólo una decisión teórica. Dependiendo de las gráficas que se obtienen, pueden verse diferentes fenómenos de relación entre las variables:
Relación lineal positiva o directa. Cuando se aumenta los valores de una de las variables, la otra también aumenta.
Relación lineal negativa o inversa. Cuando una de las variables aumenta y la otra disminuye.
No hay relación entre las variables. Cuando las variables son independientes, tales como el salario que obtiene una persona y su estatura (debe verse que la relación no puede establecerse de manera clara).
Hay relación pero no es lineal. Esto puede ocurrir, por ejemplo, si se tienen datos que se elevan hasta cierto punto para después bajar, y las variables se relacionan en cada uno de esos intervalos. Estos tipos de relaciones no serán estudiados en este curso, ya que requieren de una explicación teórica más profunda.
Para analizar la relación lineal de las variables y resumir el gráfico de dispersión es necesario hacer uso de la covarianza.
covarianza.
Es una medida de la asociación lineal entre dos variables. Dependiendo de su valor, indica la tendencia de la relación de las variables. Se denota σxy y se determina mediante la formula:
Se puede observar los comportamientos:
Si la covarianza es positiva, entonces se tiene una relación lineal positiva.
Si la covarianza es negativa, entonces se tiene una relación lineal negativa.
Si la covarianza es cero, entonces no existe relación lineal entre las variables.
Con la lista de los datos es posible calcular la covarianza en Excel por medio de la función es igual a =COVARIANCE.P( ). Siguiendo con ejemplo, ya sea con la resolución de las operaciones o con ayuda de la función en Excel, el gráfico de dispersión es σxy =0.00078. Al ser positiva se obtiene lo que se veía en la gráfica, una relación lineal positiva.
Entonces la covarianza indica el tipo de correlación lineal, pero no da información sobre que tan fuerte es la relación. Para ello se hace uso del coeficiente de correlación.
Coeficiente de correlación.
Es usado para medir la fuerza de la relación lineal entre dos variables. Se denota por r, y también se conoce como coeficiente de correlación de Pearson. Y la manera de calcularlo es:
Donde σxy es la covarianza en tanto que σx1, σy son las varían<a de los dos diferentes tipos de datos. El valor del coeficiente de correlación oscila entre –1 y +1. Según su valor se puede afirmar:
Si r=0 no hay correlación lineal entre las variables (puede ser de otro tipo).
Si r=1 existe correlación lineal positiva perfecta.
Si 0 <r <1 existe correlación positiva, y mientras mas cerca este de 1 es mas fuerte, asi como si esta mas cerca de 0 es más débil.
Si r=-1 existe correlación lineal negativa perfecta.
Si –1 <r <0 existe correlación lineal negativa y es más fuerte en la medida en que el calor se acerca a 1.
La figura siguiente muestra de forma general el posible comportamiento de la gráfica de dispersión según su coeficiente de correlación:
Hasta ahora, en Excel existe una función que permite calcular este coeficiente y solo necesita de la lista de los datos de cada variable por separado. Esta función es =COEF.DE.CORREL(datos x, datos y). Para el ejemplo de las alturas de padres e hijos puede calcularse la desviación estándar de las dos variables, teniendo:
![clip_image002[13] clip_image002[13]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhwDY6iv3WTf31utDFlEgaF1AAwc_hk1hyuK8BZwH3j6dQMglYzDMUFsicPBqHBEOO3hx_Pve9JufsDKlyKUxBYprh4lEE02fiNzjiPo26mTWB_GV5WeM9G4o1uF4hfDIu6mDStsinXU6PT/?imgmax=800) Con lo cual existe una correlación lineal positiva y fuerte. Si se quiere estudiar la dependencia entre las variables x y y, de manera que la variable se ve como dependiente de la variable x. Para realizar ese estudio es posible estimar o pronosticar la relación de causalidad, siendo necesario un valor de determine si la variables x es buena para explicar estadísticamente la variable y. Así, esta medida es conocida como coeficiente de determinación.
Coeficiente de determinación.
Se representa por r2 , y de hecho es el cuadrado del coeficiente de correlación. Sus valores van de 0 a 1; mientras que la variable x esté más próxima a 1, es mejor para explicar a y. Por otro lado, si el coeficiente de determinación es cercano a 0, entonces el valor de x no afecta de manera importante el comportamiento de la variable y. Es posible determinar este coeficiente directamente en Excel elevando al cuadrado el coeficiente de correlación.
En el caso del ejemplo de la estatura de padres e hijos, el coeficiente de determinación es r2=0.8195. De esta manera, se puede decir que existe un relación significativa que hace que la altura del padre sea factor determinante de la estatura de los hijos. Este resultado dice que, en efecto, la gráfica de dispersión se comporta muy parecido a una recta de manera muy fuerte: ¿como se traza esta recta? En el caso de apoyarse totalmente en Excel o similares, existe una forma de ajustar automáticamente la recta que mejor se aproxima a los datos: una vez creada la gráfica de dispersión y teniéndolo seleccionado en la pestaña de “Diseño”, se toma la opción “Agregar elemento gráfico” y luego selecciones “Línea de tendencia” y eliges la opción deseada. El ajuste lineal al ejemplo de las alturas resulta.
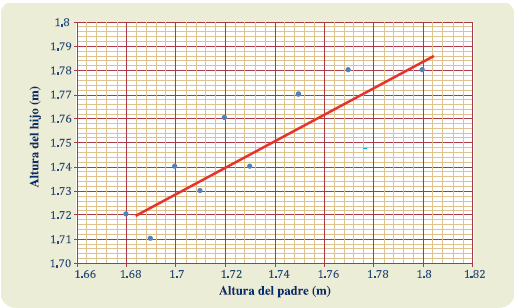
Esto es claro con toda la ayuda de Excel. Sin embargo, es posible aproximar la recta que ajusta mejor a los datos. Este proceso es conocido como regresión lineal. En general, la teoría de regresión universal permite hacer predicciones basándose en la dependencia de datos pasados de las variables y es de gran importancia en la estadística.
Regresión lineal de covarianza.
La regresión lineal permite definir la recta que mejor se ajusta a la nube de puntos. La ecuación que define cualquier recta es y = ax + b; por lo tanto, es necesario determinar los valores de a y b para que la recta quede completamente definida, los valores que se deben tomar son:
Regresando al ejemplo que se tenia sobre estaturas, la pendiente de la recta y la ordenada al origen están dadas por:
Entonces, la ecuación de la recta que se ajusta a los datos es y=0.6094+0.6958, quedando la gráfica:
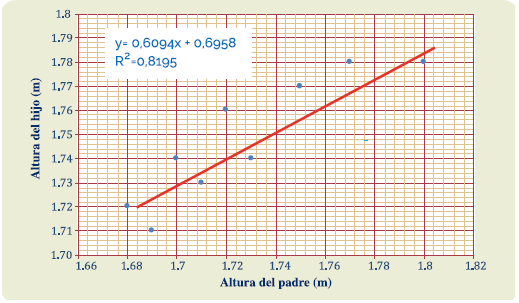
En la aplicación del programa Excel la regresión lineal es la misma que la que se calculó arriba. Su uso, como te puedes dar cuenta facilita mucho el análisis estadístico. Ahora bien, el siguiente método para usar un conjunto de datos es de los más empleados en varias áreas de la matemática. Este el es método de mínimos cuadrados.
Métodos de mínimos cuadrados.
Este método es usado por Excel para ajustar los datos. El método lo que hace es considerar que y=f(x). En otras palabras, existe una relación de causalidad entre las variables, donde la función de la recta es la que mejor ajusta los datos. El siguiente paso consiste en establecer que para cada Xi. se determina el error (e) entre la aproximación f(xi) y el valor de la variable yi esto es:
Entonces, lo que se busca es minimizar el valor de la suma del cuadrado de todos los errores (ei):
De ahí, se deriva su nombre, mínimos cuadrados. En general, si los valores del coeficiente de determinación son cercanos a 1, ambos métodos arrojaran resultados similares.
La importancia de tener la regresión lineal es para poder estimar los valores de una de las variables, sabiendo que hay cierta relación entre ellas. Una vez más recurriendo al ejemplo de estaturas, si se quisiera estimar la estatura de un hombre sabiendo que su padre mide 1.60m, se puede evaluar en la recta por lo tanto: y=0.6094(1.69)+0.6958=1.67084. Esta puede ser una buena estimación a un valor experimental. Las aplicaciones de este proceso son muy variadas. Por ejemplo, en economía y finanzas se buscan relaciones entre el índice de precios y las cotizaciones en la bolsa o el precio del petróleo y el oro, etc., con el fin de predecir cual podría ser el valor en un futuro. Sin embargo, los procesos en esta área en general suelen ser mas complejos porque intervienen muchos factores, por lo que una relación lineal rara vez ocurre y es necesario establecer relaciones de otro tipo. Pero se trata de procedimientos similares con la misma idea de la regresión lineal detrás de ellos.
| 


![clip_image002[26] clip_image002[26]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhUw5g7akKY-iHQtHXFzCB4ov4GfX1dEVRs8E_JfG-3wGojKG9QbI8Zy4G-esiYyWsirlVhy5KBBWzAGXlKp7DJ6IYl3opNWIHd428SIAVtS3HhbiIxV5GBkPYfvTeaXNe0rPQRBrKSHqOx/?imgmax=800) Un ejemplo de uso es cuando se recorre la misma distancia varias veces, la media armónica de las distintas velocidades con que se realizo cada recorrido, da la velocidad promedio global. Considera el siguiente problema:
Un ejemplo de uso es cuando se recorre la misma distancia varias veces, la media armónica de las distintas velocidades con que se realizo cada recorrido, da la velocidad promedio global. Considera el siguiente problema:![clip_image002[32] clip_image002[32]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgFcFtmCe8qiMx_eHS2umgLgy3G-FdfDd-TXv9EPKvv5UP_lDRqxWdxOYV-u-6Od_YE7zdFamfGUv1D_rXvPCpWnL48no8YSik9RZu_1zRhcI2Epl3XPbv7Gumwiv3MW2cpHIt3_WDT5y_t/?imgmax=800) El resultado no se obtuvo únicamente con promediar las velocidades, pero es posible llegar a él por medio de la media armónica de las velocidades.
El resultado no se obtuvo únicamente con promediar las velocidades, pero es posible llegar a él por medio de la media armónica de las velocidades.
![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhR-TeYuoo3tw-GJRrgHi-Mo3K3MFY5MGa-35CS3oLjWUBMbOiiAbmnnlgwlWbqFu26gzo9k7PSbTxt0MkYjPICpu5oB7JwM5c_4O7doXsYo-29-sUQpIfr0CClMFVUJmSw4q9pfeBapuBw/?imgmax=800)
![clip_image002[6] clip_image002[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj1sGn2EDtY8ZXjwQm-DBzYm_7GHVZl6rNoshdTzm-U9y76g-HdpR6FwTiVeWnFZE6_Z5asNNjswcyw8ZVlxEG7akwVCl2XXrffuDaXILJTUx-7ksoTT1EL7QjpEQJ487jZRUhBmDlRBXb8/?imgmax=800)
![clip_image002[28] clip_image002[28]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEijQ01u2j2Z9Yzzl2hp8Zb8abcezfqQtpcgClE-Zfy_0I4oCYdKbPHb-gdMb79DghbRUC3cgeuynoEUiZ6cDZQIUR1e0fRWErMe9mvFl8d6iwsnyajRgzzItTKt1rXVlAgmWUzvv4DuyZYD/?imgmax=800)
![clip_image002[30] clip_image002[30]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhxQUqLHonM6l204pm0Qz-2C6gttYTs9sIgODQSwBtFihmQ5OG7DIQ7Wb80wZUEaVItHYoJRYPLElMpA0Su5ItjEl08xeAhPqRbpCxOJlOeiMkWnimO8DqL62L53Glhtj6lJD0J9g7Dkqfw/?imgmax=800)
![clip_image002[34] clip_image002[34]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEidjLY0E3kmkJPYKu6Sbb3gk3Y4LqH3bXAkWpOL94rUr2bwCREuYZFpoNxhL3OyqgJw5PcUOhiJebMEL4iN4zA7ViTyTuonXgLIIpR7vJOuE9egeWHnbCMxnKMr4YwCaXj__nvJu3Evdpyc/?imgmax=800)
![clip_image002[38] clip_image002[38]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEitnQnTaZZpAgZsllfAxHqgNl3J08aJpuYRWB6gG3RGrig2y3xrOQY_IDly3bGwtM703-8QWC05A_8EwmFsGFiQyhWND_rq-18FDbNQFaynby8HNALaxRnngRM5r83ifcktK1efKDQPHWR8/?imgmax=800)
![clip_image002[40] clip_image002[40]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhU6kuA2aoMPK1PWNROSin0dJrlGAuVZcGMMnsOkrv6fIlAQFdl_m42audlK2FnNcX8uUlAXAhh0h9lIvFKFCczuwS1qhHc8VgminOFoCVl9Ec-hoa90VM3AAvQpIxg7kMOLDUMVTGeQKdq/?imgmax=800)
![clip_image002[42] clip_image002[42]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhZvC-nApikmQK4hXfg1KU5RyQLpwdeHCSOXUihyphenhyphenMKn3JKXuusavTLxUxx3g3GKtH_0suXRkUFo1Gy8_XK4LWElLqw8jexPxUfj6AD2IqT8jloEItPyaUYTb2OW-GquwRoBR1qTAueOmUSA/?imgmax=800)
![clip_image002[44] clip_image002[44]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjKe4WS7EUE4EoADNl3ylEx_nOSCgLFJmnPxD88zWvtDGDpkLeSHhNXZyHNON0-sGkLHM8Voq8fR7bQNSPpyxM8DEQoS6waou8UIq7SjJ6CFAcaYUuxDKGlq0baNezP7xWrgbRKObex0eBD/?imgmax=800)
![clip_image002[1] clip_image002[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjeb2WO99VcHzyChKqprLC_fJx9YoJJe8pkCRVDJ-ezSF5ahZaO3p801K63nn3DNDgYHqn7SQOCQW8abCCROh2c_2XqmkQudSxymIHxaJYXbCdB5ZU27ZjYu9IHruBRIASQqBYkR-GPsvwq/?imgmax=800)

![clip_image002[9] clip_image002[9]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh7WdtZQZrW7ZgHbnunJ4P-3IKEf_VWveqnpwRPO-GQJZFOdRSPdpgyIdvoBK_xAppvgwFrN8ASTK6AvKDSQ-G7ahE_RW8wcc9pOpXKzwEcHxj4wkvwYvVuBNN9dSUSQQ9fW0CTNySi2p3S/?imgmax=800)

![clip_image002[11] clip_image002[11]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgOogpzL2gH5HCBH8WTpT4d0dIqfvMaZN9YQTj0O9wCL7q5rUfpKcetilf06LNDI0fQ_qNrLqUF83ICjikwVXO_T5GXWr1aVuvtXRszDjbBo-mkAmkTR8jrG7UJ9L56LfQL5cYTr_9s2eko/?imgmax=800)

![clip_image002[13] clip_image002[13]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhwDY6iv3WTf31utDFlEgaF1AAwc_hk1hyuK8BZwH3j6dQMglYzDMUFsicPBqHBEOO3hx_Pve9JufsDKlyKUxBYprh4lEE02fiNzjiPo26mTWB_GV5WeM9G4o1uF4hfDIu6mDStsinXU6PT/?imgmax=800)

![clip_image002[17] clip_image002[17]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhNOFg_HR75dr7gRCpM7AmwAg1eIVUo3xAkABnLpWEjsnF_Knc-SRXv2xaJQNVaR3j325wOk8FJL2T3dPWdeY1ILm4c20XM_MGOeUMC-fJHn6mCnd8VIHiMWUNrHhn6vtL6z-z8sRXfxpaV/?imgmax=800)
![clip_image002[21] clip_image002[21]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjh5PNwInCa5XFf9uyMZaukmlVK8n9Nl4sQf0IaD_sQHH45wUtg2ok6qkVv-K3m8wmU9qT3u7oOR5zPys5XDJk-fOelROW_U-GlaaDgjFw4Q09pl4_sZDm3ehCu584CreTVxK0Hd7Woefeh/?imgmax=800)

![clip_image002[25] clip_image002[25]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjj9i5YzZtHe6M4R8g21wZn5V7TqTBGbhIXdbgAkLbOZxWXktVcjVhMXUNi5U9Kue1_rrXiCLYefD2x4b-xwrhCzaUjWzgG-LTY2tPwTbid6JDAIKc0C3zIElXs7UpnVhlQQ8h87PAlCO5i/?imgmax=800)



No hay comentarios.:
Publicar un comentario