Polinomiales

Los polinomios permiten expresar una serie de cantidades de forma simbólica. Por ejemplo, en una tienda hay varios tipos de dulces con diferentes precios: los de menta cuestan $6.00 cada uno y los de cereza $8.00.

Si se desea saber cuánto hay que pagar por la compra de X cantidad de dulces de menta y una cantidad Y de cereza, se puede hacer con la expresión:

Si se compran 4 dulces de menta y 31 de cereza, entonces se evalúa el polinomio, lo cual consiste en sustituir los valores de X y Y.

Es decir, la cantidad que se tiene que pagar es de $272.00. Esto se puede hacer sin polinomios, pero cuando manejas la abstracción puedes resolver más problemas desde diferentes ángulos. Ahora, imagina que solo tienes cierta cantidad de dinero, por ejemplo $76.00, con la cual podrías comprar 11 dulces en total. ¿Cuántos dulces se tiene de cada uno? También se pueden calcular, variando las cantidades para obtener la respuesta, de manera intuitiva o por aproximación sucesiva. Sin embargo, las matemáticas permiten buscar la solución de la siguiente manera:

Donde f es la cantidad que se tiene que pagar y h representa la cantidad de dulces, en este caso se tiene que f(x,y)=76 y h(x,y)=11.

Entonces el problema queda expresado como:

La solución para las incógnitas son:  x=4  y  y=7

En este caso resultó ser un sistema de ecuaciones con dos incógnitas. Sin embargo, existe una gran cantidad de expresiones algebraicas como:

Una expresión algebraica basada unicamente en potencias enteras no negativas, de una o mas variables, que no contienen variables en un denominador se llama polinomio. Por ejemplo:

Estas funciones son muy importante en matemáticas porque cualquier otra se puede aproximar como una función polinomial de cierto grado, como la siguiente:

Una función es polinomial si se puede escribir de la siguiente forma:

Donde los coeficientes a_{n ,} an-1 , a₀ son números reales y los exponentes n, n-1, etc., son números enteros. El grado de la función es n.

Funciones polinomiales con su grado
Función polinomial	Grado
	1
	2
	3
	13

Los nombres de cada término son importantes porque la mayor parte de las explicaciones están basadas en estos términos y conceptos.

Donde ax⁷ es el término con el grado del polinomio, bx es el término lineal y c es el término constante.

Para obtener las soluciones de las ecuaciones se usan diferentes métodos. Una raíz de la función y=f(x) es un valor x₀ que hace que f(x₀)=0. La raíz de la función también se conoce como solución de la función.

Como recordatorio, es conveniente mencionar la interpretación geométrica de las raíces de la ecuación cuadrática, las cuales están relacionadas con la fórmula general.

La función polinomial de tercer grado es aquella que se puede escribir de la forma siguiente:

La función polinomial de tercer grado más sencilla es:

Para que y=0 se requiere que x³=0. Esto quiere decir que para encontrar los números que al multiplicarlos tres veces se obtenga cero, se observa que el único que satisface esta condición es el cero. la única raíz de la función. En este caso, se dice que la raíz es de grado tres.

La siguiente función polinomial.

Se empieza por calcular las raíces, donde en la función se emplea cero. Se observa que la factorización quedaría:

Esto indica que los valores para que se elabore la función es:

Por lo que la función tiene tres raíces.

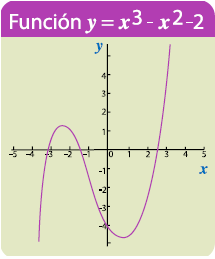Para la función y=x³ se observa que los valores negativos de x son muy grandes, los valores de y son negativos, los valores de x son muy grandes y positivos. En general, para cualquier función polinómica de grado impar, para valores suficientemente grandes de x positivos, los valores de y serán del mismo signo que el coeficiente principal de la función.

Igualmente, para los valores suficientemente grandes y negativos de x, los valores de y tendrán el signo opuesto al que tiene el coeficiente principal de la función.

Un ejemplo de una función polinómica de grado par es y=x⁴+1, la cual no tiene raíces reales, además de que cuando x=0, la función y=1.

El polinomio, al ser igualado a cero, obtiene la función:

Entonces

donde i es la parte imaginaria.

El ejemplo anterior sirve para ilustrar que solo los polinomios de grado impar tiene al menos una raíz real y que los de grado par es posible que no tengan raíces.