Método geométrico para obtener la recta tangente.

La manera más natural de la recta tangente a f(x) en un punto es la recta que mas se parece a la función en el punto, porque hay muchas rectas que cruzan por el punto a. En la siguiente figura se muestra como pasan muchas rectas por un punto f en a.

La única recta tangente es la línea roja, las demás solo son líneas que pasan por el punto pero no son tangentes.

Recordar que la pendiente es:

La pendiente de una recta a una función es:

Ahora si se toma el límite de la pendiente:

Se tiene la pendiente a la recta tangente de la función. En el punto (a,f(a)).

Se llama incremento en una variable la diferencia entre dos de sus valores, y se denota con la letra griega mayúscula delta Δ.

Ejemplo: 170- 150 –20 –Δx incremento de la estatura (cm) de una persona.

Intuitivamente significa “cuánto cambia por cada unidad que cambia x en el intervalo de 1x-2x”

La recta tangente tiene otra aplicación en otras áreas como la física donde se puede calcular la velocidad media dada como:

La velocidad instantánea es el límite de la velocidad media cuando a tiende a cero.

En la figura se muestra la relación de cambio entre el incremento Δx, donde su posición es t+Δ en el eje x y en el eje y=f(t+Δx).

Si n=f(t) número de individuos de una población. El cambio del tamaño en el tiempo. El cambio de población de t=t₁ y t =t₂ es Δn = (t₂) - (t₁), de modo que la rapidez del crecimiento durante el periodo t₁ ≤ t ≤ t₁ es:

Y a partir de esta rapidez promedio, al hacer Δt→0 se obtiene la rapidez instantánea
del crecimiento:

La razón de cambio, así definida, es válida en un intervalo. Por eso lleva el nombre de promedio, sin embargo , existen otra razón de cambio.

Se llama razón de cambio instantáneo de la función y por cada unidad que cambia x al límite de las razones de cambio promedio. Cuando el incremento en x tiene a cero:

Y su significado intuitivo es cuánto cambia por cada unidad que  cambia x en el instante x₀.

Se llama razón de cambio de la función (promedio) con respecto de x, al cociente de los incrementos:

Ejemplo:

Una polilla tiene un vuelo rectilíneo hacia un eliminador eléctrico. Su posición en el tiempo t puede determinarse mediante la función f(t)=0.7t²+2, con medido en segundos y f(t) medida en metros.

• Calcula la razón de cambio promedio de su posición (velocidad promedio de 1 a 3 segundos:

La polilla voló a una velocidad promedio de 2.8 m/s del segundo 1 al segundo 3

• Calcula la razón de cambio instantáneo (es decir, velocidad instantánea) al tiempo 2.5:

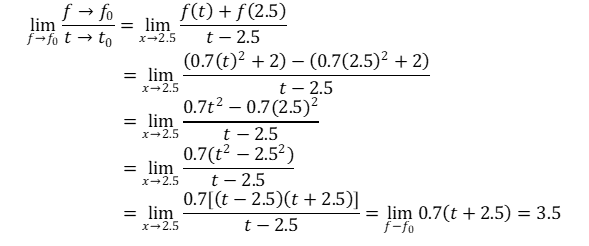
A los 2.5 segundos la polilla volaba a una velocidad instantánea de 3.5 m/s. En lo cotidiano se determinan las razones de cambio de diversas situaciones de tipo natural, social, económico. En particular, interesa conocer un mínimo o un máximo valor o cómo aumenta o disminuye ese valor en un intervalo de tiempo específico. En general, se busca reflexionar sobre fenómenos que es necesario describir o cuantificar sus cambios por medio de modelos matemáticos, gráficas y tablas.

El modelo de una población está dado por R(t) = 5000 + 500 t − 50t², donde t es el número de años después del 2000. Calcula la razón de cambio promedio de:

a) t = 2 at = 4                                b) t = 2 at = 3                                 c) t = 2 at = 2.5

a) La razón de cambio promedio de t = 2 at = 4 está dado por:

b) La razón de cambio promedio de t = 2 at = 3 está dado por:

c) La razón de cambio promedio de t = 2 at = 2.5 está dado por:

El crecimiento promedio en el lapso de tiempo del primer inciso fue la mayor con 200 hab/año, por lo cual, se concluyó que el crecimiento en el segundo año debió ser menor a 200.

En el primer semestre del año t-2 el crecimiento era de 275 habitantes por año. Así que todo parece indicar que en el primer lapso, la población aumentó rápidamente al comienzo que al final. Como se puede ver, se habla de la velocidad, donde este es un concepto físico estrechamente ligado a la tasa de cambio promedio y de derivada.

Reflexiona lo siguiente: la razón de cambio promedio se ha determinado calculando la pendiente para pareja de puntos, cuando la función decrece las pendientes de las rectas secantes son positivas, las pendientes de las rectas secantes paralelas a la abscisa es cero y las pendientes, cuando la función decrece son negativas.

En matemáticas escolares la razón de cambio más usada es la velocidad: v=d/t (distancia recorrida por unidad de tiempo). La velocidad es la razón de cambio ejemplar o prototipo. Por analogía, se le llama “velocidad” a un razón de cambio cualquiera. Por ejemplo, en problemas de proporción inversa. Estos términos dan los conceptos para el tema de derivada.

Planteamiento:  En un tanque cónico, por ejemplo, fluye agua a razón de 8 m³/min. Si la altura del tanque es de 12m y el radio de la base mide r, donde r es arbitraria pero fija.

Problema: ¿Qué tan rápido sube el nivel del agua cuando el recipiente de es de 4m de altura?

Al hacer un esquema, se puede llegar a lo siguiente:

La cantidad del agua que está en el recipiente depende de la forma geométrica. en este caso, por ser un cono, el volumen es:

Donde h es la altura del agua. Ahora hay que poner el volumen en una sola variable, en este caso h. Entonces hay que relacionar a con ℎ, con proporciones:

Hay que hacer notar que el volumen depende del tiempo, esto es: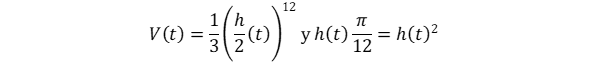
Esto es, para cada tiempo se tiene un volumen. Derivando se tiene:

Sólo falta sustituir y obtener los valores buscados. Como lo que se quiere es conocer dh/dt, donde la altura cambia dv/dt=8, esta es la razón por la que fluye el agua. Por lo tanto, se tiene que: