Máximos y mínimos.

Un problema de optimización en matemáticas consiste en maximizar o minimizar una función real eligiendo valores de entrada. De forma general, la optimización es conseguir los mejores valores de una función. Una de las principales herramientas para encontrar los valores máximos y mínimos absolutos de una función es la derivada.

Un valor es un máximo local de f si existe un intervalo abierto (a,b) que contiene a c, tal que f(x)≤f(c) para todo x en (a, b). El valor es un mínimo local si existe un intervalo (a,b) que contenga a c, tal que ƒ(c)≤ƒ(x), para todo x en (a,b).
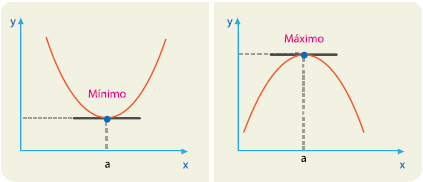
Si una función ƒ tiene un máximo o un mínimo local en un número c de un intervalo abierto, entonces ƒ’(c)=0 o bien ƒ no existe. Los puntos donde ƒ’(c)=0 también se llama puntos críticos, como se puede ver en la figura:

Se muestran dos curvas donde la recta negra es la pendiente de la función en el punto a; es decir, son los puntos críticos de la función, los cuales se encuentran en el lugar en el que la pendiente de la función es cero, dicho en otros términos, donde la pendiente de la tangente m=ƒ’,(a)=0. La idea es encontrar ese lugar geométrico en el que la pendiente de la función es cero.

Ejemplo:

Calcular los puntos críticos de la función:

Lo primero es derivar la función:

¿Donde m=f’(x)=0?

Es donde 3x²-12=0 factorizando 3(x+2)(x-2)=0 para que esta ecuación sea igual a cero se tiene que (x−2)=0 o (x+2)=0, entonces x−2=0 o x+2=0, de tal modo que:

con estos dos puntos se resuelve la función:

por lo tanto, el valor x₁=2 es un número mínimo y x₂=-2 es un máximo.

Ejemplos de máximos y mínimos.

Se desea construir una caja de cartón sin tapa con base rectangular a partir de una hoja rectangular de cartón de 16x21, recortando un cuadrado en cada esquina y doblando los lados hacia arriba.

Problema: Calcular el lado del cuadrado para el cual se obtiene el volumen máximo.

Cada lado del cuadrado mide x, un lado mide 16-2x y el otro lado mide 21-2x, entonces el volumen queda expresado como: =(16-2)(21-2)=2(168-372+23)

Esta ecuación expresa el volumen V como una función de x. Ahora se buscan sus máximos y mínimos, entonces se deriva:

Entonces los números críticos son x₁=283 y x₂=3. Como x₁ está fuera del rango, el único valor crítico es x₂=3. Por lo tanto para obtener una caja de volumen máximo se tienen que cortar cuadrados de 3cm de cada lado.