Concepto de circulo unitario
Observa estas imágenes de la historia de la rueda.
Como podrás darte cuenta, la rueda ha evolucionado de acuerdo con el tipo de material con el cual esta elaborada, pero la forma es la misma.
En una forma similar, en esta lección, vamos a utilizar el círculo unitario para definir las funciones SENO y COSENO.
Para estudiar movimiento y localizaciones en círculos es conveniente fijarnos inicialmente en su forma más simple.
El círculo unitario es el que tiene de radio 1, centrado en el origen del plano cartesiano. Su ecuación es:x2 + y2 = 1
El circulo unitario tiene la propiedad de que su radio es igual a la unidad. Al obtener los lados de una línea que gira y describe un ángulo, las dimensiones del triángulo que se forma al proyectar una vertical y la distancia horizontal por donde corta esta vertical representan las funciones trigonométricas seno y coseno: seno para el lado vertical del triángulo y coseno para el lado horizontal del centro a la distancia en la que corta con la vertical.
Ejemplo
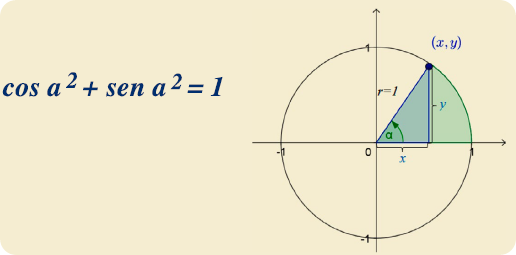
Para cualquier punto (x, y) en el círculo unitario podemos construir un triángulo rectángulo, como se muestra en la gráfica de abajo. Nota que los catetos corresponden a las coordenadas X y Y del punto respectivo. La hipotenusa es el radio del círculo unitario.
Por la ley de Pitágoras, sabemos que:
x2 + y2 = 12 entonces x2 + y2 = 1
Por la definición de las funciones sen y cos tenemos
y = sen α y x = cos α
Reemplazando estas ecuaciones en la fórmula de arriba, tenemos que: