Aplicaciones de la recta tangente.

En física, la recta tangente se aplica para calcular el incremento de una variable. Se llama incremento en una variable a la diferencia entre dos de sus valores, y se denota con la letra griega mayúscula delta Δ.

Por ejemplo, 170–150=20=Δx incremento de la estatura (cm) de una persona. Esto significa “cuánto cambia   por  cada unidad que  cambia x en el intervalo de x1 - x2 ”.

Tenemos dos conceptos:

1. La velocidad media dada como:

2. La velocidad instantánea, que es el limite de la velocidad media cuando Δt tiende a cero.

Observa la siguiente figura, en donde se muestra la relación de cambio entre el incremento Δx, donde  su posición es t + Δx en el eje x y en el eje y = ƒ( t + Δx ).

Ahora considera lo siguiente:

= ƒ(t ) es el número de individuos de una población.
El cambio del tamaño en el tiempo es t .
Entonces, el cambio de población de t=t₁ y t=t₂ es Δn=ƒ(t₂ ) - ƒ(t₁), de modo que la rapidez del crecimiento durante el periodo t₁ ≤ t ≤ t₂ es:
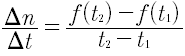Y a partir de esta rapidez promedio, al hacer t—>0 se obtiene la rapidez instantánea
del crecimiento:
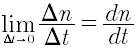La razón de cambio definida asi es válida en un intervalo, por eso lleva el nombre promedio, sin embargo existen otra razón de cambio.
Se llama razón de cambio instantáneo de la función y por cada unidad que cambia x al límite de las razones de cambio promedio. Cuando el incremento en x tiende a cero:
Esto significa cuánto cambia por cada unidad que cambia en el instante x₀ .
Se llama razón de cambio de la función (promedio) y con respecto de x, al cociente de los incrementos.

Considera el siguiente ejemplo para comprender lo anterior:

Una polilla tiene un vuelo rectilíneo hacia hacia un eliminador eléctrico. Su posición en el tiempo t puede determinarse mediante la función ƒ(t)=0.7t²+2, con t medido en segundos y ƒ(t) medida en metros.

a) Calcula la razón de cambio promedio de su posición (velocidad promedio) de 1 a 3 segundos.

La polilla voló a una velocidad promedio de 2.8 m/s del segundo 1 al segundo 3.

b) Calcula la razón de cambio instantáneo (es decir, velocidad instantánea) al tiempo 2.5

A los 2.5 segundos la polilla volaba a una velocidad instantánea de 3.5m/s.

De manera cotidiana se determinan las razones de cambio en diversas situaciones de tipo natural, social y económico. Particularmente se interesan por conocer un mínimo o máximo valor o como aumenta o disminuye ese calor en un intervalo de tiempo específico. Pero, en todos los casos, se busca reflexionar sobre fenómenos que son necesarios describir o cuantificar sus cambios por medio de modelos matemáticos, gráficas y tablas.