Los teoremas o leyes del seno y coseno se aplican en
triángulos oblicuángulos (en los
cuales ninguno de sus ángulos es recto).
Ley de
seno. Los lados de un triángulo son
proporcionales a los ángulos de los senos opuestos (Baldor 1993; pág.
372)
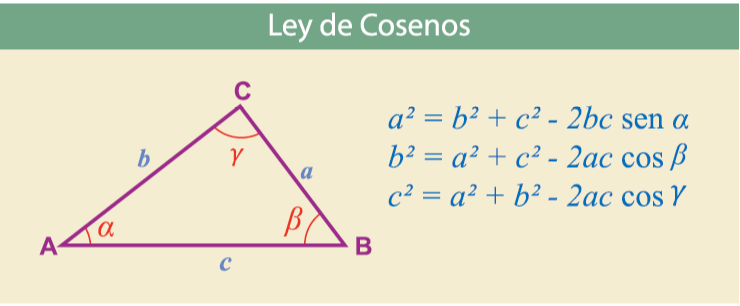
Ley de
coseno. El cuadrado de un lado de un
triángulo es igual a la suma de los cuadrados de los otros, menos el duplo del
producto de dichos lados, por el coseno del ángulo que forman (Baldor, 1993;
pág. 373)
Las leyes de seno y coseno son herramientas matemáticas
para resolver problemas de física, uno de ellos es utilizado para calcular la
fuerza resultante entre dos fuerzas. El método empleado se llama paralelogramo
y es para vectores concurrentes cuyo proceso analítico hace uso de estas
leyes.
La resultante de un sistema de vectores es el vector
que produce el mismo efecto que los demás vectores del sistema. Por ello, un
vector resultante es aquel capaz de sustituir un sistema de
vectores.
Ejemplo.
Encuentra la fuerza resultante de las fuerzas aplicadas
a una caja para ser removida.
| | |
Donde c es
la Resultante, a
él cateto o lado, b el otro cateto
o lado y q
el ángulo que forman los vectores a
y b.
Y para hacer el “calculo analítico”, primero se debe
calcular la magnitud y también la dirección.
a) Calculo
de la magnitud.
b) Calculo
de la dirección.
Para calcular la dirección se utiliza la ley de los
senos.
Regresa al ejemplo anterior.
Resultado.
Las leyes de seno y coseno permiten calcular la
resultante, cuando las fuerzas que se aplican forman triángulos oblicuángulos;
evitan utilizar otros métodos más complejos como dividirlo en dos triángulos
rectángulos para después usar las funciones trigonométricas o aplicar el método
gráfico para vectores concurrentes.



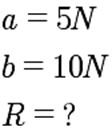
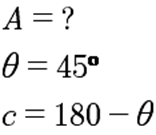
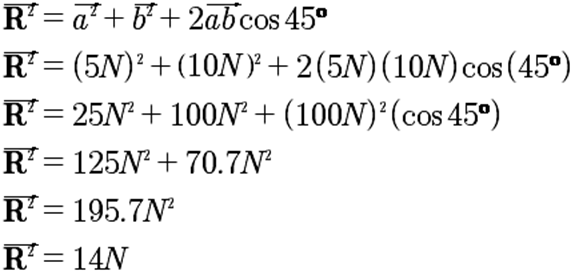






No hay comentarios.:
Publicar un comentario