Una interpretación de la derivada de la función en un punto es la pendiente de la recta tangente a la gráfica de la función en el punto (x0f(x0)). Debes saber que la recta tangente ademas ademas de ser la línea que toca la gráfica solo en un punto, también es la única que está realmente cerca de la gráfica de la función.
Esta propiedad permite usar a la recta para aproximar el valor que toma la función en valores cercanos al punto donde se construyó la tangente. Para empezar, como recordarás, la recta tangente a la función f(x) en un punto x0 está dada por:
 En la figura se muestra cuan próximos están la gráfica de la función con la recta tangente para la función f(x)=x3 en x=1.
En la figura se muestra cuan próximos están la gráfica de la función con la recta tangente para la función f(x)=x3 en x=1.
En la ecuación anterior, el término x-x0 es el cambio en x, y puede ser denotado por Δx. Cuando este cambio es pequeño, la variación en y, denotado Δx, puede
aproximarse mediante el uso de la recta tangente como sigue:
La cantidad Δx, suele denotarse dx, y es llamada diferencial de x. La expresión
ƒ’x(dx) se denota , denominado diferencial de y.
En general, puede definirse dx, el diferencial de x, como cualquier número distinto de cero, usualmente muy cercano a cero, y dy=ƒ’(x)dx , el diferencial de y.
De acuerdo con la notación de Leibniz, la derivada
de una función y=ƒ’(x) está dada por:
En general, puede definirse dx, el diferencial de x, como cualquier número distinto de cero, usualmente muy cercano a cero, y dy=ƒ’(x)dx , el diferencial de y.
De acuerdo con la notación de Leibniz, la derivada
de una función y=ƒ’(x) está dada por:
 Pensando en que los términos en dy/dx se expresa como una división, el diferencial que quedaría definido mediante el despeje de dy. Este razonamiento no es correcto del todo, dado que pese a que tienen notación similar a la regla de la cadena, puede escribirse como:
Pensando en que los términos en dy/dx se expresa como una división, el diferencial que quedaría definido mediante el despeje de dy. Este razonamiento no es correcto del todo, dado que pese a que tienen notación similar a la regla de la cadena, puede escribirse como:
Esa formula puede parecer completamente correcta pues como se está dividiendo y multiplicando por el mismo diferencial puede simplificarse. Esta afirmación no es correcta, pero la ecuación que resulta si lo es. Debes ser cuanto pues en los textos es común escribir sin mucho cuidado el razonamiento que hay detrás, pues al escribirse las formas diferenciales presentan un comportamiento acorde a lo que se puede esperar. La recomendación es que siempre hay que tener en cuenta el significado detrás de estas afirmaciones.
Cabe mencionar que las fórmulas de derivación pueden escribirse en forma diferencial. Por ejemplo, si u y v son funciones de x, los diferenciales resultan:
De esta manera, se pueden escribir las formulas para las funciones y operaciones de funciones más comunes. Por ejemplo, la forma diferencial del producto se calcula como:
 Todos esos cálculos, aunque ya se han hecho para derivadas, se encuentran resumidos en la siguiente tabla:
Todos esos cálculos, aunque ya se han hecho para derivadas, se encuentran resumidos en la siguiente tabla:|
Formulas
diferenciales
| |
|
Suma o resta
|
|
|
Producto
|
|
|
Cociente
|
|
Entre las aplicaciones de los diferenciales se encuentran:
- Estimar el valor de Δy ≈ dy o el valor de una función en valores cercanos a uno
que se conoce - Estimar el error en mediciones.
- Para mostrar el procedimiento de cada una de estas aplicaciones se consideran los siguientes ejemplos:
Estimar el valor de Δy
Para este tipo de aplicación es necesario que se proporcione la función y el valor de dx.
Sea y = x3, determinar dy cuando x=1 y dx=0.01.
Para y=ƒ(x)=x3 se tiene que ƒ’(x)=3x2, entonces el diferencial de y se calcula dy=ƒ(x)=dx=ƒ’(1)(0.01)=3(0.01)=0.03.
Para complementar el ejemplo calcularemos el valor de Δy.Δy = ƒ (x + Δy) −ƒ (x ) = (0.01)3 − 1 = 0.030301
Como puedes ver, estos valores son muy cercanos pues hay una diferencia de 0.000301, que ciertamente es muy pequeño. Pero cuando Δx o dx tienden a cero, los valores de d y dx se aproximan cada vez más.
Aproximar el valor de una función:Para aproximar una función y = ƒ (x) se puede hacer uso de la fórmula:ƒ (x + Δx ) ≈ ƒ (x) + dy = ƒ (x) + ƒ ´ (x)dx
Esto no es más que un despeje de la fórmula establecida en el ejemplo 1. En éste se usarán diferenciales para aproximar:
Primero obtengamos el dx, que según la figura 2 se puede calcular como:
Como la distancia entre el punto donde se calcula la derivada y el punto que se necesita es de 1, entonces dx=1, y de acuerdo a la fórmula:
Los valores de f(x) y la recta tangente son muy parecidas, a saber:
En resumen, los diferenciales y las rectas tangentes pueden se usados para estimar valores de la funciones en puntos cercanos a alguno de ellos, del cual se sabe el valor exacto. Es por esto que son de gran utilidad en la práctica, ya que puede ser muy complicado evaluar las funciones directamente. De hecho, las matemáticas aplicadas se dedican a hacer estudios sobre teoría de aproximaciones y son la base de muchos de los avances científicos y tecnológicos actuales.
Error propagado.En tiendas en línea se pueden comprar instrumentos que aseguran una gran precisión al momento en sus medidas. Por ejemplo, se puede comprar un calibre de Vernier, el cual es un instrumento para realizar medidas de objetos pequeños. Uno de ellos permite tomar medidas de hasta 150 mm, con un error máximo en la medición de 0.01 mm, esto según el fabricante.Si con el calibre mencionado anteriormente se mide la arista de un dado, obteniendo 1.7 mm y suponiendo que todas las aristas miden lo mismo ¿Cuál es el error que se propaga al volumen del dado?
En este caso, la fórmula para hallar el volumen de un cubo está dado por
V=a3, donde a es la arista del dado. Entonces a=1.7 y −0.01≤Δa≤0.01.
Para aproximar el error propagado se deriva V en términos de a y se
aproxima ΔV.
Entonces el error propagado por la medición del calibre es ±0.0867 mm3.
Esta cantidad puede parecer pequeña pero si el volumen total de es 2mm3, por ejemplo, esto representa casi la mitad, lo que haría un error extremadamente grande. Para estudiar el error extremadamente grande. Para estudiar el error con respecto a la magnitud que se considera, se hace el uso del error relativo, esto es comparando dV con V como sigue:
 La proporción dV/V es el error relativo. En este caso es ±0.0176. Es muy común presentar el error en términos de un porcentaje, conocido como error porcentual. Este se obtiene multiplicando el error relativo por 100%. El error porcentual en este ejemplo es de 1.0176%
La proporción dV/V es el error relativo. En este caso es ±0.0176. Es muy común presentar el error en términos de un porcentaje, conocido como error porcentual. Este se obtiene multiplicando el error relativo por 100%. El error porcentual en este ejemplo es de 1.0176%
Como puedes ver, el error propagado no es más que la variación posible que puede tener el valor de la variable independiente con respecto al cambio que sufre la variable independiente, de ahí que pueda ser estimado por medio de diferenciales.
Gran para del trabajo de la Física-Matemática y en particular, de las matemáticas aplicadas, radica en encontrar funciones que permitan describir el comportamiento o desarrollo de un fenómeno físico en la naturales para hacer proyecciones a futuro y tomar las medidas necesarias.
En el caso de la estacionalidad en fenómenos naturales y sociales. Por ejemplo en los fenómenos naturales la temporada de lluvias o en el caso de fenómenos sociales: los gastos de las familias que responden a temporadas navideñas o festejos como el día de las madres (los cuales se presenta como una línea ondulatoria). Sin embargo, en la teoría se obtiene cantidades que ninguna computadora es capaz de operar o manejar.
Por esa razón, la teoría de aproximaciones juega un papel muy importante para obtener resultados tan cercanos al real como sea necesario. Los diferenciales pueden ser considerados como un primer acercamiento a este tipo de trabajos y, además, presentan una aplicación palpable del calculo. Estos son temas de interés para muchas personas que no alcanzan a ver toda la utilidad práctica que pueden tener.
Por supuesto, como herramienta tan compleja, es natural que los problemas que pueden se atacados con ella sean de un nivel mucho más alto. DE ahí la dificultad para presentar eventos cotidianos donde se usen.

![clip_image006[4] clip_image006[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgOhPW1sVpLOXOhq6sPj__zb01WBq6hX1S33IxjKUiZTUMHwngd9PgHxssQ9fxE4JghBNQj_b7fVm85zsbMMc6J1hYx9yZ33t3IZgHQcWbFxuy_bcMS-lIa2nk1c0as82Wg9Byf97zx3Bp3/?imgmax=800)
![clip_image004[6] clip_image004[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgkLA7IGcVgqPFnZGpiYoE2d5oBqKiyl3aUhXdtULWlsHTc2WVbmbIkpxOwCFo6GIpgJmreoHfN79-jHtdn8HEoquQw8FSgPxWfWLBh6NHh6M8TCC_TI15hkcsrzkrsFenWa-de6GAxhVkr/?imgmax=800)

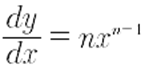



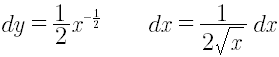







No hay comentarios.:
Publicar un comentario