En los siglos XVI y XVII se plantearon problemas cuyo fin era resolver la forma en que varia una cantidad a otra, como en la Física. Estos problemas impulsaron el surgimiento del Calculo Integral y, en consecuencia, del Calculo diferencial. El calculo es la parte de las matemáticas que estudia el movimiento y el cambio. El calculo nació del desarrollo de cuatro problemas planteados en el siglo XVII:
- El problema de la tangente.
- El problema de la aceleración.
- El problema de máximos y mínimos.
- El problema del área.
Ejemplo:
Para producir 500 toneladas de jitomates se necesitan:
Se usa la función cx=2x2-6x.
- ¿Cuanto deberá pagarse por 30 toneladas la producción, es decir, reproducir 530 toneladas de jitomate?
Primero se identifican las derivadas.
 Para obtener el costo de producción de 30 toneladas usaremos la operación derivadas teniendo en cuenta x=500 ton tenemos lo siguiente:
Para obtener el costo de producción de 30 toneladas usaremos la operación derivadas teniendo en cuenta x=500 ton tenemos lo siguiente:
El costo de 530ton=556,820.00
Concepto geométrico
El concepto de
derivada es sugerido geométricamente, en principio mediante la noción intuitiva
de la tangente a la curva y=f(x) y un punto fijo
P(a,f(a)) en ella. Si se toma otro punto Q(b,
f(b)) en la curva y se traza una secante
lPQ ocupara las diversas posiciones de P
y Q’ · P y Q”, etc. Con la
aproximación por la curva del punto Q al punto
P, la secante lPQ tiende a ocupará
la posición de una recta determinada, la cual se llama tangente a la
curva en el punto P. Esta tangente es caracterizada por el
ángulo α entre su dirección y el eje x
positivo.
En la grafica, la recta
l intersecta a la función f=(x) en los puntos
P(a,f(a)) y Q(b,f(b)), donde la recta forma el
ángulo α respecto al
eje x, por lo que la tangente
α es:
 Pero Δy = ƒ(b) -
ƒ(a) y Δx = b - a; por lo tanto, la pendiente de la
secante l de la
Pero Δy = ƒ(b) -
ƒ(a) y Δx = b - a; por lo tanto, la pendiente de la
secante l de lacurva está dada por:
Si se designa al límite con
m, la ecuación de la recta tangente es:
![image_thumb[4] image_thumb[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgtKH8Ks_UrJsGPTOT4XBlFOm4iowtr1zw7cwDoHxulXAeLCWShMrXnNRcVyYkX9_81kEGoH_yrK2PvJXHSEaRBPotECUE6t0Z1uAZf8Y9j1AHEMACSTtsVUjfMvGkbb5XWA1EDhRcA5AFN/?imgmax=800) Nótese que la tangente a una curva en
un punto se define como el límite de las secantes a esa misma curva se pasan por
ese punto, y no como la recta que “corta” a la curva en un punto.
Nótese que la tangente a una curva en
un punto se define como el límite de las secantes a esa misma curva se pasan por
ese punto, y no como la recta que “corta” a la curva en un punto.
Ahora sea
f(x) una función en intervalo abierto que contiene al número
real . En la figura de la derecha se muestra la gráfica de f
y una recta secante
lPQ
que pasa por P(a, ƒ (a)) y Q(x, ƒ (x)). La
recta de trazo punteado l representa una posible recta tangente en el punto
P.
La pendiente m
de l es el valor límite de la
pendiente lPQ
cuando tiende a P, de tal forma que:
![image_thumb[6] image_thumb[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj0kflIzmZskIrC9rD-j_fnjMkAibGn264m3cOGSTE2yID7s9QoGOxJDp1u0vdEYakvxlfR3xeHB2qGzRzM90W3KazlzeaqwMXqK4TsuKRJqwS1UmT0m7Mb7010BkBeFvm5p-Rvil5X5hHf/?imgmax=800) Si x≠ a, entonces
existe un número real ℎ≠0, tal que x=a+ℎ (es
decir, ℎ = x−a), como se muestra en la figura.
Si x≠ a, entonces
existe un número real ℎ≠0, tal que x=a+ℎ (es
decir, ℎ = x−a), como se muestra en la figura.Y la pendiente m será:
Este límite es uno de los
conceptos fundamentales del calculo y se llama derivada de la función
f en a.
Sea f una
función definida en un intervalo abierto que contiene a a. La
derivada de f en a, denotada por
f’(a), está dada por:
Si, este límite existe.
La notación
f’(a) se lee f prima de a.
Cuando f’(a) existe, significa que el limite existe, y
se dice que la función f es derivable en a o
que f tiene derivada en a.
Como razón de cambio
La derivada es útil en muchas aplicaciones, tales como estudiar y medir cantidades que varían con el tiempo. Si t es el tiempo y f(t) es la medida de una cantidad física, por ejemplo:
- f(t) es la distancia recorrida por un automóvil desde un momento inicial t0’.
- f(t) el numero de habitantes de una población de un país o un cultivo de bacterias.
- f(t) el volumen de agua de una represa.
La variación que ha sufrido la cantidad f(t) en el tiempo transcurrido desde t0 hasta t y la razón:
Es la variación que ha sufrido esa cantidad por unidad de tiempo transcurrido, es decir, la razón de cambio de la cantidad que se está midiendo.
Ejemplo:
Si f(t) es la distancia recorrida por un automóvil que se mueve en línea recta, entonces la razón de cambio es la velocidad media del automóvil en el lapso de tiempo de t0 a at. Si se grafica la función f(t), donde en el eje x se ubica a la variable del tiempo t, y en el eje y a la variable de distancia d, entonces se obtiene una curva, como en la siguiente figura:
La pendiente m de la secante a esta curva por los puntos P y Q, es:
 Si el carro se desplaza con un movimiento rectilíneo uniforme a velocidad constante, entonces el gráfico es una recta, la cual coincide con la secante y la velocidad es la pendiente de la secante.
Si el carro se desplaza con un movimiento rectilíneo uniforme a velocidad constante, entonces el gráfico es una recta, la cual coincide con la secante y la velocidad es la pendiente de la secante.
Ahora, sea w una variable que es un función del tiempo, tal que se tiene w=f(t), donde f es una función derivable. LA diferencia entre el valor inicial y el final de w en el intervalo de tiempo [t, t, +h] es (t+h)-f(t).
Si w=f(t), donde f es derivable y t representa el tiempo, entonces:
- La tasa o razón media de variación de w=f(t) en el intervalo [t, t+h] es:
- La tasa o razón de variación de w=f(t) con respecto a t es:
Las unidades que deben usarse dependen de la naturaleza de la cantidad representada por w. A veces se llama a dw/dt la tasa o razón instantánea de variación de w con respecto a t.
Si un punto se mueve sobre una recta coordenada l, de manera que su coordenada al tiempo (t) es s(t) (se muestra a continuación), donde s(t) es la función de posición de P
La aceleración a(t) de P al tiempo t se define como la tasa de cambio de la velocidad con respecto al tiempo, es decir:
Si P es un punto sobre una recta coordenada de l, tan que su posición al tiempo t está dada por s(t), donde s es una función derivable, entonces:
- La velocidad v(t) de t al tiempo es v(t) =s’(t).
- La rapidez de P al tiempo es |v(t)|.
- La aceleración a(t) de P al tiempo t es a(t) =v’(t)=s”(t).
Por lo que se llama función velocidad de P y a es la función de la aceleración de P. Se utiliza también la notación:
 La función de posición de un punto P que se mueve sobre una recta esta dada por:
La función de posición de un punto P que se mueve sobre una recta esta dada por: No siempre la variable es el tiempo. Por ejemplo, si en física o química se estudia una solución en un recipiente al cual se le agrega un líquido, la variable x puede ser el volumen total de líquido y f(x) la masa de ese volumen. Como la razón masa/volumen es la densidad, la razón de cambio es:
No siempre la variable es el tiempo. Por ejemplo, si en física o química se estudia una solución en un recipiente al cual se le agrega un líquido, la variable x puede ser el volumen total de líquido y f(x) la masa de ese volumen. Como la razón masa/volumen es la densidad, la razón de cambio es:
La cual es la densidad del volumen agregado a la solución.
Obtención de una derivada.
Cuando f es derivable para todo x, asociando a cada el número ƒ’(x), se obtiene una función f’ llamada derivada de f. El valor de f’ en x esta dado por el siguiente límite:

El número x es fijo pero arbitrario y el limite se toma haciendo tender h a cero. Derivar f(x), significa determinar a f’(x).
Sea la función f(x)-2x3+4x2-4, encontrar f’(x) 1. Derivada de la función constante.
1. Derivada de la función constante.Si la función constante definida por f(x)=c para todo:
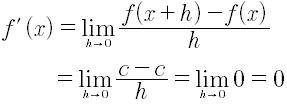
2. Derivada de la función identidad (variable independiente).
Si para todo f(x)=x, para todo x, entonces:
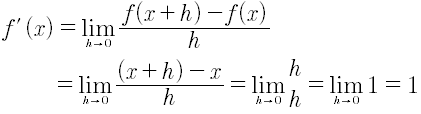
3. Derivada de la función potencia.
Sea f(x)=xn, entonces:
 Usando el Teorema del Binomio:
Usando el Teorema del Binomio: Todos los términos después del primero contienen un factor h elevado a alguna potencia entera. Restando xn y dividiendo entre h se obtiene:
Todos los términos después del primero contienen un factor h elevado a alguna potencia entera. Restando xn y dividiendo entre h se obtiene:
Como todos los términos dentro del paréntesis, excepto el primero, contienen una potencia de h, la derivada queda como:
Dada la función y=x4, encontrar dx/dy
 4. Derivada de una función por una constante.
4. Derivada de una función por una constante.Sean f(x) y g(x) funciones y una constante, donde g(x)=c·f(x), entonces:

Para el caso especial f(x)=cxn, al derivar cxn se multiplica el coeficiente c por el exponente n y se le resta 1 al exponente original.
La función y=5x4, encontrar f’(x).
Sea f(x), g(x) y k(x) funciones, donde k(x)=f(x)+g(x), entonces:

Ejemplo:
Encontrar la f’(x) de la función f(x)=3x4+4x2-2x2-x
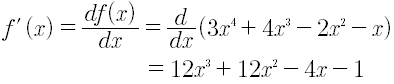 6. Derivada de un producto de funciones.
6. Derivada de un producto de funciones.Sean f(x), g(x) y k(x) funciones, donde k(x)=f(x) · g(x), entonces:

Para cambiar la forma del cociente de manera que el límite pueda evaluarse, se suma y resta la expresión f(x+h)g(x) en el numerador. Entonces:

Lo cual puede escribirse así:
 Como f es derivable en x y también es continua en x. por lo tanto limh→0 ƒ(x
+ h) = ƒ(x). También limh→0 g(x), ya que x se mantiene fijo al tomar el límite.
Finalmente, aplicando la definición a ƒ(x) y g(x) se obtiene:
Como f es derivable en x y también es continua en x. por lo tanto limh→0 ƒ(x
+ h) = ƒ(x). También limh→0 g(x), ya que x se mantiene fijo al tomar el límite.
Finalmente, aplicando la definición a ƒ(x) y g(x) se obtiene:
Así la regla del producto puede enunciarse como sigue: “La derivada de un producto es igual al primer factor multiplicado por la derivada del segundo, más el segundo factor multiplicado por la derivada del primero”.
Ejemplo:
Encontrar la ƒ´(x) de la función ƒ(x) = (x2 + 2) (x2 + 4x - 3) usando la regla
del producto:

En este ejemplo también se puede evaluar f’(x) multiplicando los dos factores x2+2y2x2+4x-3 y derivando el polinomio resultante.
7. Derivada de un cociente de funciones.
Sean f(x), g(x) y k(x) funciones, donde k(x)=f(x)/g(x), entonces:
 Restando y sumando g(x)f(x) en el numerador del último cociente resulta:
Restando y sumando g(x)f(x) en el numerador del último cociente resulta: O, equivalente:
O, equivalente:
Tomando el límite del numerador y el denominador se obtiene la regla del cociente:
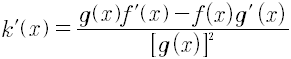 Esta regla del cociente puede enunciarse: “La derivada de un cociente es igual al denominador multiplicado por la derivada del numerador menos el numerador multiplicado por la derivada del denominador, todo ello dividido entre el cuadrado del denominador”.
Esta regla del cociente puede enunciarse: “La derivada de un cociente es igual al denominador multiplicado por la derivada del numerador menos el numerador multiplicado por la derivada del denominador, todo ello dividido entre el cuadrado del denominador”.Encontrar la dy/dx de la función, usando la regla del cociente.:

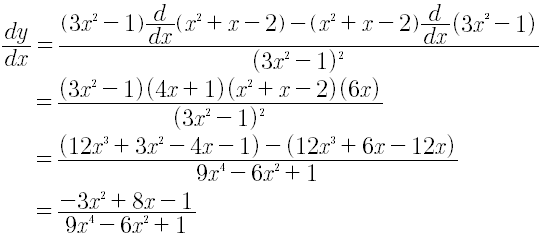
8. Derivada de la función potencia con exponente negativo.
Sea f(x)=x-n, entonces usando la definición de x-n y la regla del cociente:
 9. Derivada de la potencia de una función:
9. Derivada de la potencia de una función:
Las reglas de derivación anteriores se usan solamente para sumas, restas, productos y cocientes de expresiones de la forma donde es un entero. Para expresiones como (2x2+2)3 no se ha presentado ninguna regla que se aplique directamente. Es claro que:
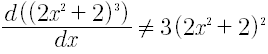 Cambiando la forma de la expresión se tiene:
Cambiando la forma de la expresión se tiene:Y entonces, derivando:

Por lo tanto:
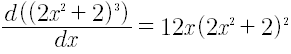 Para estas expresiones es conveniente tener métodos mas sencillos para calcular la derivada. El que se usa en este caso sirve para expresar como una función compuesta de , es decir, si ƒ y g son funciones, tales que:
Para estas expresiones es conveniente tener métodos mas sencillos para calcular la derivada. El que se usa en este caso sirve para expresar como una función compuesta de , es decir, si ƒ y g son funciones, tales que:
Por lo que es una función de ƒ. Esta última es la función compuesta ƒ º g. Ahora
que y=(2x2+2)3 puede expresarse de esta manera, definiendo:
El objetivo es encontrar una fórmula para la derivada dy/dx de la función compuesta dada por:
10. Regla de la cadena.
Si y=ƒ(u), u=g(x), y las derivadas dy/du y
du/dx existen ambas, entonces la función
compuesta definida por y=ƒ(g(x)) tiene una derivada dada por:
 Ejemplo.
Ejemplo.Usando la regla de la cadena, encontrar la dy/dx de la función y=(3x2+7x-5)5.
Considerando:
Donde se expresa a y como una función compuesta de x. Entonces, por regla de la cadena:

11. Derivadas de las funciones logarítmicas.
a) Sea u, una función donde ƒ/x) = loga u, entonces:
b) Sea u, una función donde ƒ/x) = In(u), entonces:
 12. Derivadas de funciones exponenciales.
12. Derivadas de funciones exponenciales.a) Sea u, una función donde ƒ/x) = au, entonces:
b) Sea u, una función donde ƒ/x) = eu, entonces:
 En síntesis, la forma de estudiar la solución de una derivada es a partir de la definición de límite y por ello se realizaron varios ejemplos de las derivadas de las funciones más importantes. Además, en el estudio de límite es importante para la verificación de una buena solución de la derivada de una función, pero el uso del calculo diferencial e integral va mas allá de su estudio matemático y permite conocer y modelar el desenvolvimiento de fenómenos naturales y sociales.
En síntesis, la forma de estudiar la solución de una derivada es a partir de la definición de límite y por ello se realizaron varios ejemplos de las derivadas de las funciones más importantes. Además, en el estudio de límite es importante para la verificación de una buena solución de la derivada de una función, pero el uso del calculo diferencial e integral va mas allá de su estudio matemático y permite conocer y modelar el desenvolvimiento de fenómenos naturales y sociales.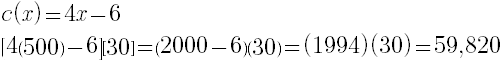
![clip_image001[4]_thumb clip_image001[4]_thumb](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj-HMmZPlpOzB76fvsQuF-ZbMaCZEIegcZQNwhnjJ6xoa7hLo7g8pF66QBZ3x2mV61x7zq8GKjB9BMTs6OSX2z6WMQGrKkcDCDCzzy5wcKK40HK4V7CihG6FaeWI6N2HhMfVwwmxuBfX_k4/?imgmax=800)
![clip_image002[4]_thumb clip_image002[4]_thumb](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhMpvYftBigWoSzgWGlHka7m4Uuf1UzjACUgaNtVVW7rAp0EF9LjIMpfUAVEL0-_jpwqQgqiMY_RSL5QnxpDXrJrIc_nvabfc449MiSNRz3IrJ-Yk00KBo8AT9MHL0WYN52Hb87ib4hDhol/?imgmax=800)
![image_thumb[1] image_thumb[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgKbXcwYSLNcK7YpphU_4q-LZ8pTD8OndnIdRah5Y7O4_K32TyrLzuD_YgUo25H11HDFUPOZWsRiAdhPfgCF6FYubUJ9zrF_qzEI_-ZY-J2I3CzI-PfGie9DJfzVHsqhtcvVhyphenhyphencHsbAVO4K/?imgmax=800)
![image_thumb[2] image_thumb[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiswOqN9ihSwNbLTlL4UxBx__FuPdleUfjo93II_u7bjW7rk1dQf9H9T6TtL42dcSTHjdMRmQgQrdE5w4gUh3UKUfsCdXyl1LGsJR_sGym4iWaFP4mhFPyzYYFQUYXXjtLMYX-sznSDJFEm/?imgmax=800)
![image_thumb[5] image_thumb[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjRypqpkB4urecH0rNvaHDGqXfzrECmEMP9vhOrtW-5bBAiAyRBD17ejzkDE7_1arQRvsk5-53L-fCHAAyvJ2XvXtLLkTHm_QONJz5dz3L3DeYTzt0jGxGKAmrs3RVmOZ3wbjwsybyeTf-T/?imgmax=800)
![image_thumb[7] image_thumb[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiM4mEZ7wKmSLB5ds0DZfuptRZvCHxwdAqt_es8gANVGbsF1v6sxlA7iQEVbblYgFXgbk3EazcmdzTrmBJMdSAH4rssXG_V3N33YkgRkLMqQDU2Bet8dH4g1gys-0cq7waxN2-1Oopcj5ww/?imgmax=800)
![image_thumb[8] image_thumb[8]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjGEFLajudGwLcr8T5aCUMgYZbr65LXVGoBNaUygmw6kJQTWvTUsKoVQj1oGqCIFE6256J32TCtgW-mWrF9tTNZo896NULgmP0BCcFpV3ZMHxV5_Q5MMWD1obRPG9h0tjmQwtbkHoalhwVn/?imgmax=800)












No hay comentarios.:
Publicar un comentario