Por medio de los métodos como el muestreo, un investigador puede obtener una gran cantidad de datos en relación al fenómeno que esté estudiando. Sin embargo, los datos por si solos no proporcionan información sobre el fenómeno, por lo que es necesario pasarlos por un proceso que los sintetice o resuma de manera que sea más sencillo interpretarlos, entenderlos y usarlos. Las tablas de distribución de frecuencias son la herramienta para organizar y tratar los datos para que permitan observar la forma de distribución.
Tablas de distribución de frecuencias.
En las tablas de distribución de frecuencia los valores de la variable, es decir, los datos (Xi) son organizados de manera ascendente o descendente junto con las frecuencia (fi) de cada dato. Es decir, el número de veces que el dato es observado dentro de una tabla. La tabla puede ser para datos no agrupados, así como para datos agrupados o de intervalos de clase.
Tablas de distribución de frecuencias para datos no agrupados.
En el caso de que los datos se apropien de un numero pequeño de valores o si la variable es discreta. Por ejemplo, cuando se toman solo números enteros, es posible acomodar los datos en una columna y sus frecuencias respectivas en la segunda, ya que la longitud de la tabla no será demasiado grande. Sin embargo, para un mayor estudio de los datos es conveniente considerar diferentes tipos de frecuencias como son las siguientes:
- Frecuencia absoluta (fi). Es el número de veces que aparece un determinado dato X en el estudio. La suma de las frecuencias absolutas siempre es igual al número de datos que se estén considerando. Usualmente el número total se representa por la letra N y el número total de variables a considerar se denota por f. Entonces:
f1 + f2 + • • • + fn = N
- Frecuencia relativa (fri). En este tipo de frecuencia se hace la proporción de la frecuencia absoluta y el número total de datos. La suma de las frecuencias relativas es igual a 1.
- Frecuencia acumulada (fai). Es la suma de las frecuencias absolutas de todos los valores inferiores o iguales al valor considerado. Por ejemplo, si hay datos ordenados de menor a mayor, …x1, x2, …, x8 y se quiere saber el valor de la frecuencia acumulada en el dato 5, la operación sería:
fa5 = f1 + f2 + f3 + f4 + f5
- Frecuencia relativa acumulada (frai). Es el cociente entre le frecuencia acumulada de un determinado valor y el número total de datos.
Para mostrar la construcción de la tabla de distribuciones de frecuencias de datos no agrupados se considerará el siguiente ejemplo:
En un salón al que asisten 30 alumnos se les preguntó cuántos vasos de
refresco consumieron en la semana anterior a la aplicación del cuestionario. Las
respuestas obtenidas de los alumnos fueron las siguientes:
{5, 6, 3, 1, 0, 4, 3, 1, 5, 5, 3, 2, 1, 2, 3, 2, 3, 4, 4, 1, 4, 1, 1, 3, 3, 1, 0, 0, 0, 2}
El primer paso para el tratamiento de los datos es agruparlos en orden ascendente, como se hizo a continuación:
{0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 6}
{5, 6, 3, 1, 0, 4, 3, 1, 5, 5, 3, 2, 1, 2, 3, 2, 3, 4, 4, 1, 4, 1, 1, 3, 3, 1, 0, 0, 0, 2}
El primer paso para el tratamiento de los datos es agruparlos en orden ascendente, como se hizo a continuación:
{0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 6}
De esta manera la tabulación de distribución es más sencilla, puesto que es más fácil contabilizar cuantas veces se repite cada valor. La siguiente tabla incluye los diferentes tipos de frecuencia, a la vez que se expone la forma de calcularlas:
|
No. de vasos que consume
|
Frecuencia absoluta
|
Frecuencia relativa
|
Frecuencia acumulada
|
Frecuencia relativa
acumulada
|
|
0
|
4
|
4/30=0.13
|
4
|
4/30=0.13
|
|
1
|
7
|
7/30=0.23
|
4+7=11
|
11/30=0.37
|
|
2
|
4
|
4/30=0.13
|
11+4=15
|
15/30=0.50
|
|
3
|
7
|
7/30=0.23
|
15+7=22
|
22/30=0.73
|
|
4
|
4
|
4/30=0.13
|
22+4=26
|
26/30=0.87
|
|
5
|
3
|
3/30=0.10
|
26+3=29
|
29/30=0.97
|
|
6
|
1
|
1/30=0.03
|
29+1=30
|
30/30=1.00
|
|
Total
|
30
|
1.00
|
30
|
|
Una vez teniendo la tabla de distribuciones de frecuencias es natural preguntarse acerca de la utilidad de esta, pues en ella es muy sencillo identificar información sobre el conjunto de los datos. Pero ¿que tiempo de información? Por ejemplo, de la tabla anterior se pueden desprender, entre otra, las siguientes afirmaciones:
- Dado que la cantidad de alumnos que tomo 5 o más vasos de refresco es de 4 y se tienen 30 datos, se puede decir que la mayoría consumió menos de 5 vasos de refresco. El porcentaje de alumnos que tomó menos de 5 vasos es de 87%.
- El porcentaje que tomo 5 vasos de refresco es de 29%.
- Ningún alumno tomó más de 6 vasos de refresco en la semana.
Como se puede notar la información es presentada de manera entendible más que la lista de respuestas a los alumnos. En realidad a lo que se dio importancia fue a dicha respuesta no a quien pertenecía. Para esta tabla la variable no era el niño sino la cantidad de vasos que tomaba, y de esta se extrajo la información.
Dado que la cantidad de variables es pequeña, se pudo registrar cada una de ellas. Existen casos en que esto resulta inapropiado para trabajar, aunque no hay una regla precisa de cuándo considerar todas las variables o cuando agruparlos. Se recomienda que si el número de datos de N es mayor de 50 o si el recorrido de la serie de datos es mayor de 20, entonces se use el esquema agrupado de datos.
Tablas de distribución de frecuencias de clase o de datos agrupados
En este caso la tabulación de los datos están ordenados en clases y aparece la frecuencia de cada una; es decir, los datos originales de varios valores cercanos en el conjunto se combinan para formar lo que se llama intervalo de clase. Por ejemplo, en lugar de tomar la edad exacta de personas, pueden tomarse intervalos de edad: de 0 a 5 años, de 6 a 10 años, entre otros.
Es más conveniente usar la distribución agrupada cuando las variables tomen valores continuos; es decir, la variable puede tomar cualquier valor entre dos números dados al realizar un experimento. Por ejemplo, cuando se están considerando mediciones de longitud de algunos objetos. Esta magnitud puede variar solo milímetros entre los objetos y no tendría caso tabular los que tienen exactamente la misma medida. Es más útil saber cuántos objetos tienen una longitud que oscila en un cierto tamaño, como puede ser entre 1 y 3 cm.
Para realizar la organización en clases se necesita un arreglo determinado de las observaciones, y para lograrlo se requiere seleccionar los intervalos de clase. Esta selección depende de los datos o del fenómeno a estudiar. Sin embargo, el método más usual para el tratamiento de la información puede contener los siguientes puntos:
- Ordenar los datos de menor a mayor para su clasificación.
- Determinar la magnitud de la variación de los datos o el rango (R) es decir, la longitud del intervalo (I) en el que están contenidos todos los datos:
R = xmáx - xmin ; I = [xmáx , xmin]
Donde xmin, xmáx son los datos de menor y mayor valor numérico respectivamente.
- El siguiente punto útil es definir la cantidad de clases, el número de clases (Nc) debe tener un tamaño razonable para poder interpretar la información en la tabla. Existen varios método para determinar este número:
Logaritmos decimales
De todas las posibles bases que pueden tomarse para los logaritmos, las más usuales son la base 10 y la base e. Los logaritmos que tienen base 10 se llaman logaritmos decimales, logaritmos vulgares o logaritmos de Briggs, y para representarlos se escribe sencillamente log sin necesidad de especificar la base:
log10X = log X
Límite real superior (Lrs ) = Ls +0.5
Para mostrar la forma de organizar los datos por medio de clases, considera el siguiente ejemplo:
En un hospital son registradas las personas que ingresan diariamente a visitar
a alguno de los pacientes. El registro fue realizado por 40 días y se obtuvieron
los siguientes datos:{30, 35, 15, 21, 18, 32, 39, 20, 19, 20, 20, 34, 13, 13, 20, 35, 30, 17, 30, 31, 10, 32, 22, 14,
30, 36, 23, 14, 20, 34, 20, 28, 20, 16, 31, 38, 22, 12, 28, 13}.
Puedes realizar la tabla de frecuencias para analizar esta información. Para empezar es necesario organizar los datos en orden ascendente:
{10, 12, 13, 13, 13, 14, 14, 15, 16, 17, 18, 19, 20, 20, 20, 20, 20, 20, 20, 21, 22, 22, 23, 28,
28, 30, 30, 30, 30, 31, 31, 32, 32, 34, 34, 35, 35, 36, 38, 39}.
Los datos toman demasiados valores, algunos de los cuales solo aparecen una vez. Esta observación implica que una tabla de datos no agrupados puede no ser apropiada para seguir con la organización de datos, por lo tanto hay que considerar usar los intervalos de clase y sus respectivas frecuencias. Para ello se encuentran los valores necesarios.
Acoplando toda la información en la tabla, el resultado es el siguiente:
|
Clase
|
Límites de clases
|
Limites reales de clase
|
Frecuencia
|
Frecuencia relativa
|
Marca de clase
|
Frecuencia acumulada
|
Frecuencia relativa
acumulada
| ||
|
No.
|
Li
|
Ls
|
Lri
|
Lrs
|
fi
|
fri
|
mi
|
fai
|
frai
|
|
1
|
10
|
14
|
9.5
|
14.5
|
7
|
0.175
|
12
|
7
|
0.175
|
|
2
|
15
|
19
|
14.5
|
19.5
|
5
|
0.125
|
17
|
12
|
0.3
|
|
3
|
20
|
24
|
19.5
|
24.5
|
11
|
0.275
|
22
|
23
|
0.575
|
|
4
|
25
|
29
|
24.5
|
29.5
|
2
|
0.05
|
27
|
25
|
0.625
|
|
5
|
30
|
34
|
29.5
|
34.5
|
10
|
0.25
|
32
|
35
|
0.875
|
|
6
|
35
|
39
|
34.5
|
39.5
|
5
|
0.125
|
37
|
40
|
1
|
Si bien las tablas de distribuciones ya son una forma más clara de organizar los datos que se tienen, también es importante presentar la información de manera más visual, esto es por medio de gráficos.
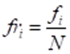
![clip_image002[5] clip_image002[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh4jqc7raZlvmcAMzVZ7-ctgVC6I0Pbczwp1K0ix1Gn9RGL77EGnb1VdwpWI9whb4O79v0gB1C4n3fwFQ3tPV9EUWj3F4e3q3Qc3rn6BxGUlRs0UoKGdZpMigoptjS89k7vOELoUhFwgpQx/?imgmax=800)
![clip_image002[17] clip_image002[17]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiTw51mNeECVPC98xyw09ifIBGt3gMG93U5gT1KotXfSvIGn47DiqyHnVY4Vle-WId9Vj_yyujw6ARzVni4fFLu4Fz9BUH_rgcfHARcmKJuvnKtEb7OjUkarsIMBQWLFSLfiFMfvXE1pSVc/?imgmax=800)


