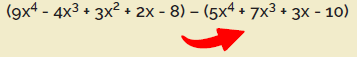Los polinomios pueden tener coeficientes reales, ser
completos o incompletos; los completos son los que tienen todos los exponentes
en orden decreciente, por ejemplo:
Suma de polinomios
Para sumar polinomios se deben sumar los coeficientes de los
términos que sean semejantes, en caso de no haber términos semejantes sólo se
escribe la suma de todos los términos de los polinomios.
Ejemplos:
Se pueden ordenar los polinomios de manera vertical,
ordenando los términos semejantes por columnas o realizar la suma de forma
horizontal identificando los términos semejantes.
a) Forma vertical
Se ordenan los términos semejantes por columnas. En caso de no
existir un término semejante en alguno de los polinomios, se completa agregando
0xn (donde n es el exponente del término faltante) para poder
respetar el lugar de ese término o bien se puede omitir, pero respetando el
lugar.
b) Forma horizontal
En cada polinomio se identifican los términos semejantes y
se realiza la suma de los coeficientes. Ejemplos:
En las sumas, se marcan del mismo color los términos semejantes
de ambos polinomios y del resultado de la suma para que puedas identificar los
términos que se sumaron. El resultado de la suma está ordenado de mayor a menor
exponente.
Resta de polinomios
Para realizar esta operación, restamos los términos semejantes
de cada polinomio. Con el fin de evitar problemas con los signos, se pueden
multiplicar los signos del polinomio al que antecede el signo menos, antes de
realizar la resta.
Nota: Se
multiplican todos los signos del polinomio por el signo menos que le antecede.
Ejemplo:
También se puede hacer de forma vertical, pero recuerda que
cada signo del sustraendo se debe multiplicar por el signo menos (-). En la
siguiente tabla marcamos con color los signos que se deben multiplicar.
En realidad, la resta sigue el mismo procedimiento que la
suma, sólo debes cuidar los signos que resultan de la multiplicación de signos.
Multiplicación de polinomios
a) Multiplicación de monomio por polinomio
El monomio debe
ser multiplicado por cada uno de los términos del polinomio.
Recuerda multiplicar los signos, los coeficientes numéricos
y en el caso de literales iguales los exponentes se suman.
Ejemplos:
b) Multiplicación de polinomio por polinomio
Para realizar la multiplicación de polinomios, se multiplica
cada uno de los términos del primer polinomio por cada uno de los términos del segundo
polinomio. Al finalizar se reducen los términos semejantes en caso de existir.
Ejemplos:
Marcaremos con un color cada término del primer polinomio y
del mismo color el resultado de multiplicar ese término por el segundo
polinomio.
División de polinomios
a) División de un polinomio por un monomio
Se realiza la división de cada
término del polinomio entre el monomio, se aplican las leyes de los signos para
división y la ley de exponentes para bases iguales.
Ejemplo:
Recuerda que la división de
exponentes dice que cuando las bases son iguales los exponentes se restan, en
este caso al mayor exponente le restamos el menor quedando de la siguiente
manera:
8z3 - 10z2 +
4z - 12 entre 2z2
b) División de polinomios
La división de polinomios sigue los
mismos principios y procedimientos que la división aritmética de números.
Pasos para realizar la división de
polinomios
1. Se escriben, tanto el dividendo como el divisor,
ordenando sus términos de forma tal que los exponentes de la misma literal
vayan decreciendo de valor. Cuando no exista el término correspondiente a un
exponente debe completarse la expresión usando un cero como coeficiente.
2. Se divide el primer término del dividendo entre
el primer término del divisor para obtener el primer término del cociente.
3. Se multiplica el primer término del cociente por
el divisor y el producto se resta del dividendo.
4. Si el residuo tiene un término cuyo grado es
mayor o igual que el término de mayor grado del divisor, se repiten los pasos
1, 2 y 3 hasta lograr que el residuo tenga un grado menor que el del divisor,
al ocurrir esto la división termina.