Esta es una de las distribuciones más usadas cuando se trata del estudio con características cuantitativas de poblaciones de individuos, como edades, peso, estatura, entre otras. En principio, este tipo de distribución es usada para variables aleatorias continuas. Es sencillo considerar variables discretas como continuas, como son la altura o el peso de las personas. Cuando se tiene una distribución continua cada elemento tiene la misma probabilidad de ocurrencia o por lo que al trabajar con este tipo de variable se debe determinar la probabilidad de que se toma en valor dentro de un cierto intervalo. La distribución normal tiene una gráfica en forma de campana, conocida como campana de Gauss o simplemente gaussiana, en honor a Carl Friedrich Gauss, quien hizo muchos estudios al respecto. La función que define la distribución normal es:
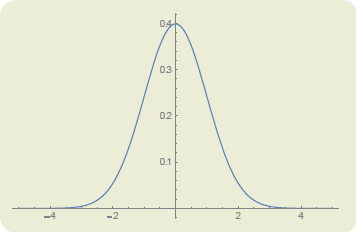
Donde µ es la media y σ la desviación estándar, la mas común es cuando µ=0 y σ=1, conocida como distribución normal estándar. La gráfica es de la forma:
Para determinar la propiedad de caer un intervalo es necesario obtener el área bajo la gráfica de la función en el intervalo que se necesita. Basados en la misma regla de las distribuciones de probabilidad se debe cumplir que la probabilidad del espacio muestral Ω debe ser P(Ω) =1, entonces el área bajo la función debe ser 1. Si se construye una función que describa variables aleatorias no negativas y cuya área bajo la gráfica sea 1 se denominan funciones de densidad de probabilidad.
Para trabajar de manera practica conviene recordar la siguiente tabla para la distribución de los datos:
|
Distancia
de la media
|
Porcentaje
de datos
|
|
|
68%
|
|
|
95%
|
|
|
99.7%
|
 De acuerdo con las propiedades de la distribución normal, 68% de los datos distan de la media a lo más en una desviación estándar, 95% están cerca de la media en a lo más dos desviaciones estándar, y la mayoría de todos los datos en 99.7%, distan a los más 3 desviaciones estándar de la media. Con esta información se pueden hacer afirmaciones respecto del comportamiento de los datos como:
De acuerdo con las propiedades de la distribución normal, 68% de los datos distan de la media a lo más en una desviación estándar, 95% están cerca de la media en a lo más dos desviaciones estándar, y la mayoría de todos los datos en 99.7%, distan a los más 3 desviaciones estándar de la media. Con esta información se pueden hacer afirmaciones respecto del comportamiento de los datos como:
Ejemplo: Se ha observado que la distribución de las calificaciones en una escuela tiene un comportamiento aproximadamente normal. Si el promedio de calificación es de 6.5 y la desviación estándar es de 1.3, entonces es posible afirmar que aproximadamente
- 68% de los aspirantes sacan entre 5.2 y 7.8.
- 95% sacan entre 3.9 y 9.1
- Y prácticamente todos, es decir 99.7%, obtienen una calificación entre 2.6 y 10.




No hay comentarios.:
Publicar un comentario